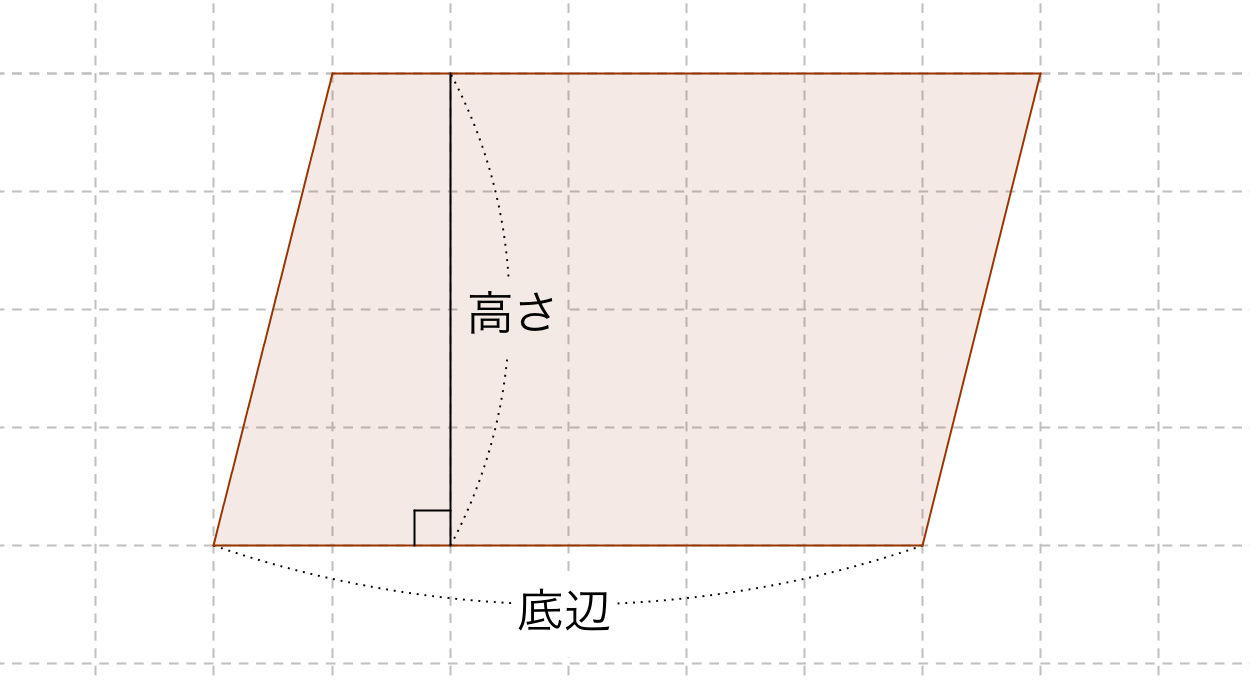
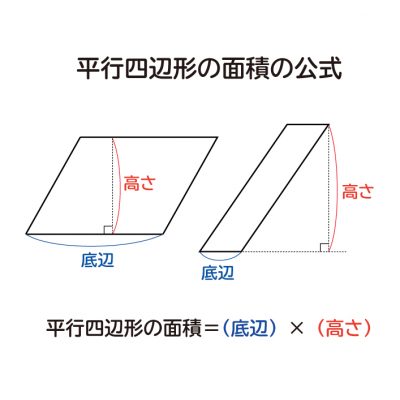
既習の面積の求め方 を基に,平行四辺形, 三角形,台形,ひし形 などの面積の求め方を 工夫して考え,公式を つくり出すことができ る。 平行四辺形,三角形, 台形,ひし形などの面 積の公式を用いて求め ることができる。 平行四辺形,三角形, ひし形(対角線直交四角形)の面積=対角線×対角線÷2 円周=直径×円周率(314)=半径×2×円周率(314) 円の面積=半径×半径×円周率(314) おうぎ形の弧の長さ=円周×中心角/360=直径×314×中心角/360ひし形の面積の公式 ひし形の面積は 2 2 つの対角線の長さをかけて2で割ったもの、つまり 『対角線×対角線÷2 ÷ 2 』 で求めることができます。
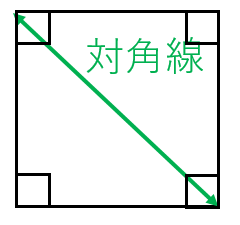
正方形の面積を求める2つの公式 具体例で学ぶ数学
公式 ひし形 の 面積 の 求め 方
公式 ひし形 の 面積 の 求め 方-ひし形の面積を求めるために,すでに学習した長方形の面積の公式を使ってみましょう。 ひし形の対角線をそれぞれ底辺と高さにした長方形を作ります。 求めるひし形以外の面積は,もとのひし形と同じ面積です。 計算方法を考えましょう。 実施時期 5年生3学期(1月) 単元項目 5−16 四角形と三角形の面積 ひし形の面積の公式 を用いれば、一瞬で面積が出ます。 求める面積は、\(6×10×\frac{ 1 }{ 2 }=30\)となります。 公式さえ覚えておけば無駄な作業や時間を省略することが可能です。
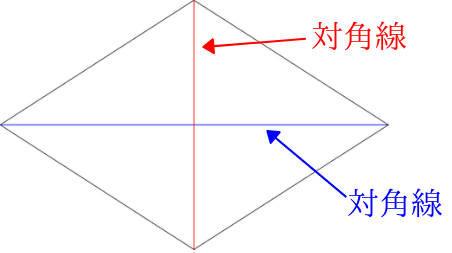



小学校で習うひし形の面積の求め方 対角線を使った公式で求められる理由 みけねこ小学校
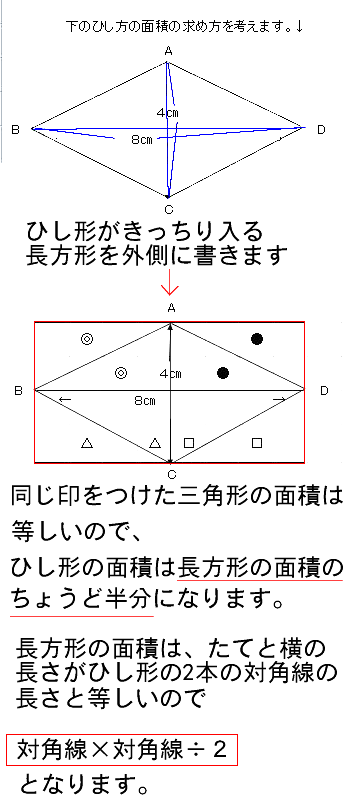
答えを簡素化する 公式を使って答えを求め、書き出しましょう。面積を求めているので適切な単位(平方センチメートル等)を使いましょう。下記を参考にしましょう。 (3√3 x 9 2)/2 = (3√3 x 81)/2 = (243√3)/2 = 48/2 = 2104 cm 2ひし形の面積を求める公式 面積=対角線×対角線÷2 対角線が10cmとcmのひし形の面積は? → 10 × ÷ 2 = 100 → 100cm 2 この公式は覚えてしまってもいいのですが、どうしてこの公式で面積が求められるかがわかるとより理解が深まります。 まず、ひし形が 角度や辺、面積を求めたり、比で表したりします。この単元では、図形の性質と基本公式をしっかり覚えておくことがポイントです。 覚えておきたい面積の求め方は、 四角形(正方形・長方形)、平行四辺形、台形、ひし形、三角形 の5つとなっています。
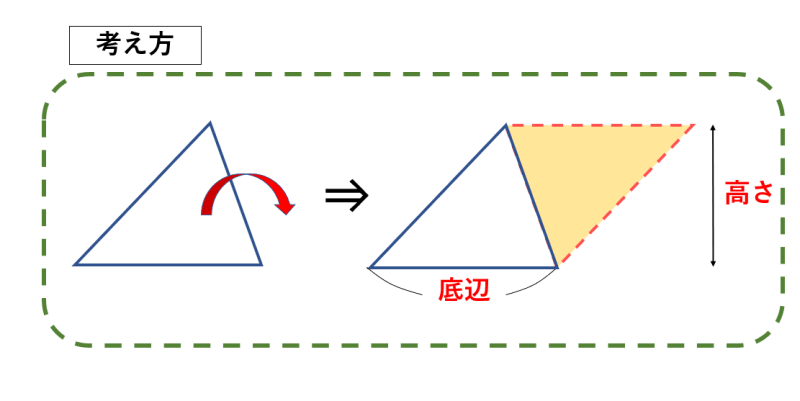
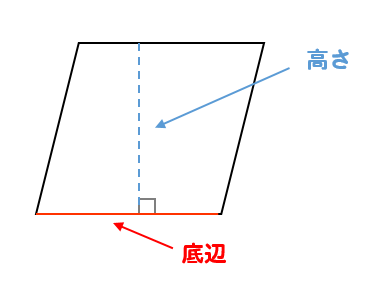
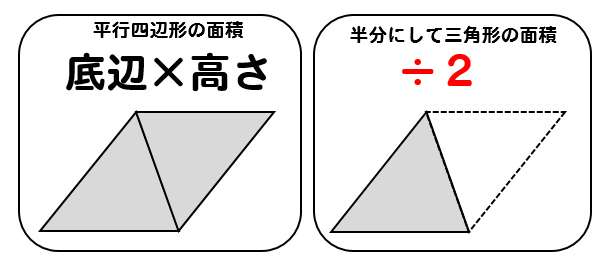
ひし形の面積の求め方が分かる。 ・ 三角形や長方形を基に、ひし形 の面積の求め方を考え、説明す る。 児童が説明する算数的活動⑤ ひし形の面積 の求め方をい ろいろ考え、説 明し、公式を導 くことができ る。(ア、ウ、 エ) ひし形の面積 の意味とその 基本的な面積の求め方・公式を解説 それでは早速、四角形や長方形の基本的な面積の求め方・公式からみていきましょう。 三角形の面積 三画形の面積 は、 底辺×高さ÷2 で求めることができます。 三角形は平行四辺形を対角線で切って半分にした形 です。同じ形の三角形を逆さまにして2つを合わせてみるとすぐ分かります。本単元の目標は,「平行四辺形,三角形,台形、ひし形などの面積の求め方を理解し、公式をつくり 出してそれらの面積を計算で求めることができる。」である。これは,学習指導要領の第5学年〔b 量 と測定〕(1)において次のように位置付けられている。 b(1
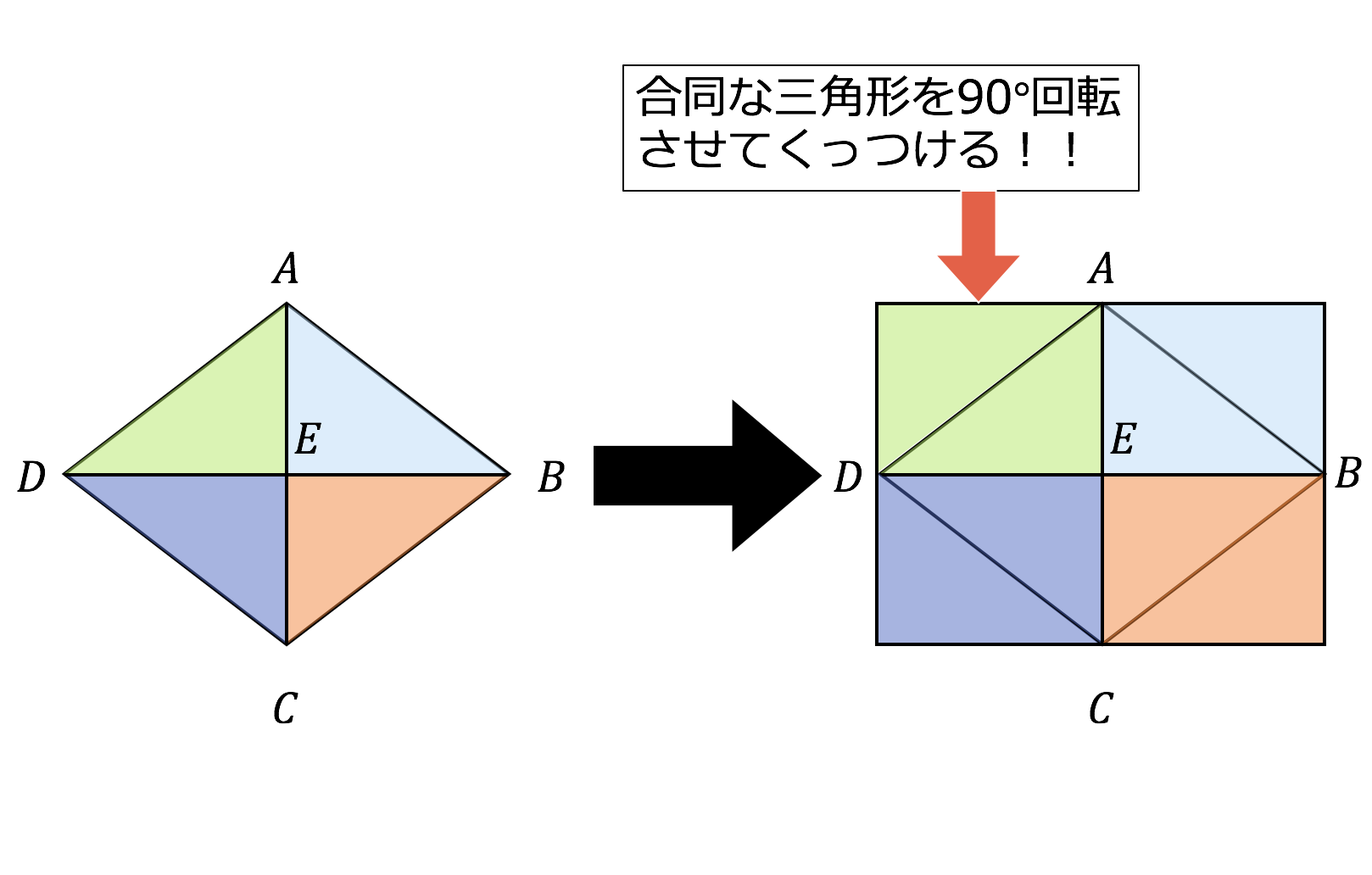
ひし形の面積の求め方を考える。 ・ 三角形や長方形を基に、ひし形 の面積の求め方を説明する。 児童が説明する算数的活動⑥ ひし形を求積 できる図形に 変形し、進んで ひし形の面積 を求めようと している。(ア、 イ) ひし形の面積 の求め方をい ろいろ考え、説 明することが できる<公式を確認する。> って、面積の公式がつくれな ひし形の面積公式=対角線×対角線÷2 いかを考えさせる。 振 3 学習をまとめる。 系統の一例 これは、ひし形を折り返して作ったものだから 面積がひし形の2倍 になっています。 つまり、この長方形の面積を求め、それを半分にすることでひし形の面積を求めることができるという
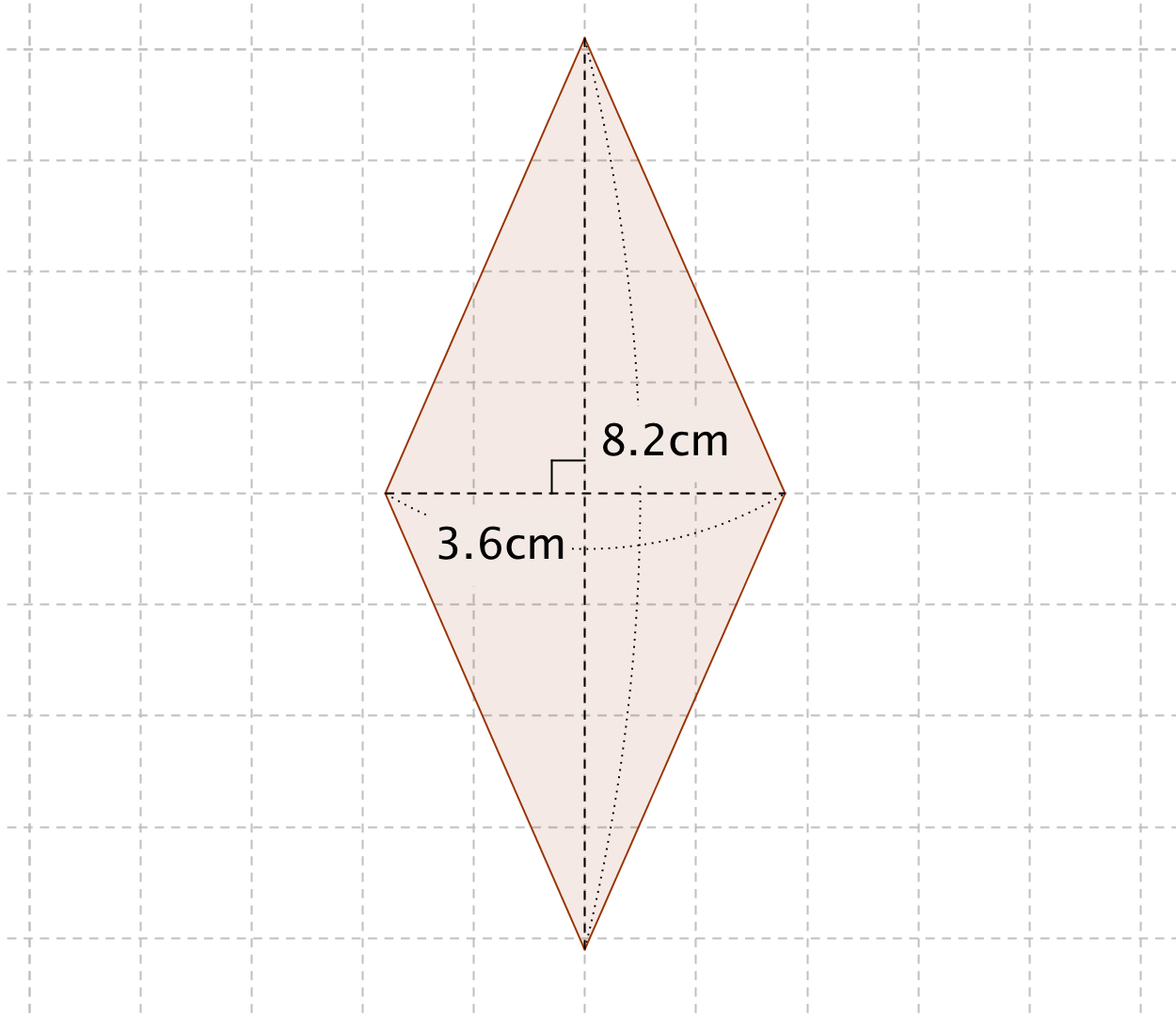



ひし形の面積の公式 算数の公式



5年算数面積2 教え方のポイント
ひし形の面積の求め方を考えることができる。 ひし形の面積を求める公式をつくり出し,それを適用して面積を求めることができる。 (2)評価規準 考ひし形の面積の求め方を,既習の図形の求積方法に帰着して考え,筋道立てて説明している。 (3)展開 十分満足できる児童への手だて ★ ひし形の面積の求め方を考える。 ひし形の面積を求める公式をつくる。 12 一般四角形の面積の求め方を考える。 13 方眼を使って不定形の面積を求める。 14 練習問題や発展問題をして、学習の定着をはかる。 6.実践紹介 (1) 前時の指導 前時は、図のような問題場面から、台形の面積の求め方の求め方とその公式 本単元 面積 ・三角形,平行四辺形の面積 の求め方 ・ひし形,台形の面積の求め 方 ⑦ 体積 ・体積の単位(cm3,m3)と 測定(5年へ移行) ・立方体・直方体の体積の 求め方(5年へ移行) ⑨ 円周と円の面積 ・円周率 ・円の面積の求め方(6年へ移行) およその形と大きさ ・およその




小学5年生 ひし形 台形の面積 算数 Active Learning 学院
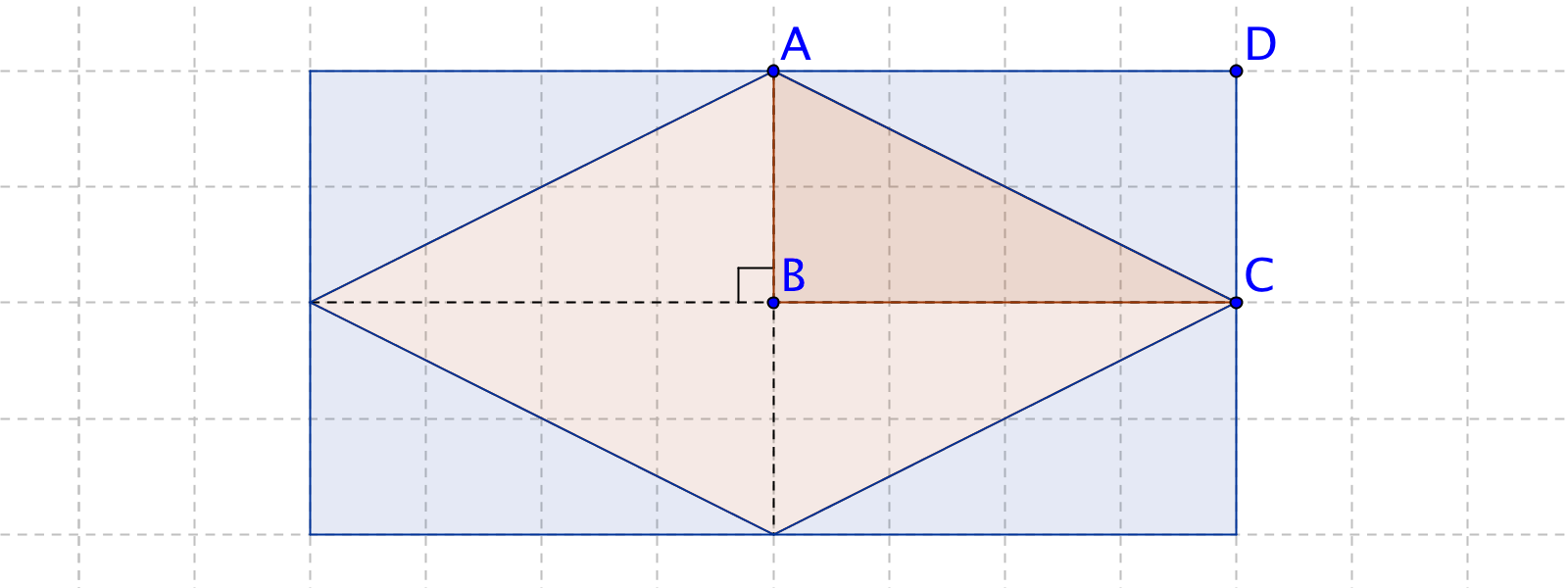



ひし形の面積の公式 算数の公式
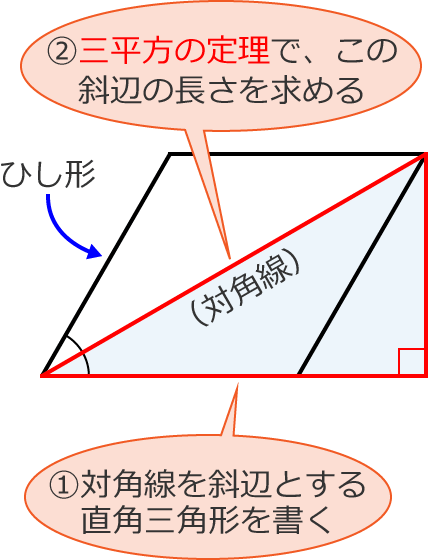
カイト 面積の求め方は、底辺×高さ、で求められる。 カイト 三角形の面積の公式は底辺×高さ÷2だ。 カイト 同じ大きさの2つの三角形を組み合わせて四角形をつくる。 カイト そんで、その四角 読者になる Active Learning 学院 新しい学びを、はじめましょう。 男子寮 図書館それでは「ひし形の面積の公式」を使った「練習問題」を解いてみましょう。「公式の考察」についても合わせてみていきます。 練習問題① 対角線が 8(cm)、4(cm)のひし形の面積を求めてください。 練習問題② 対角線が 36(cm)、(cm)のひし形の面積を求めてみましょう。 公式のしたがって、 = の公式で面積を求められます。 また、どちらか1辺の長さが分からない場合でも、斜辺の長さが分かれば、この公式を使うことができます。斜辺は直角と向かい合った一番長い辺です。長さが分からない辺は三平方の定理 =)を使って求めることができます。 例えば、ある直角




ひし形の対角線の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



ひし形の面積 高精度計算サイト
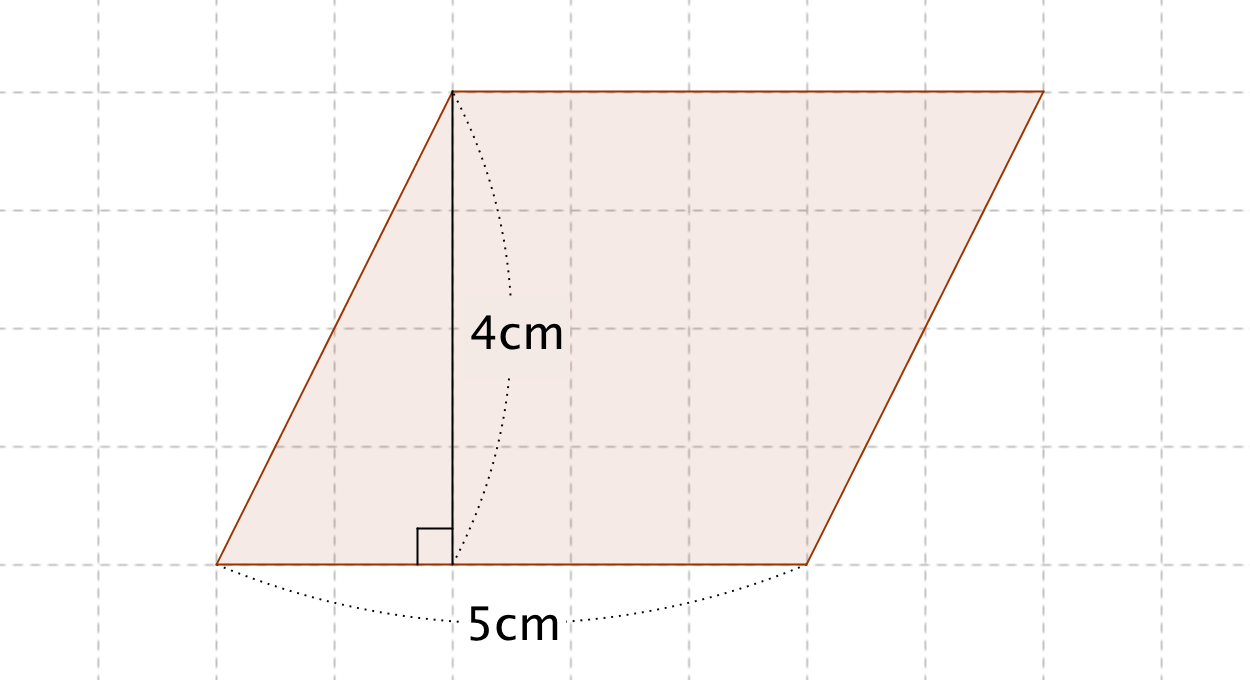
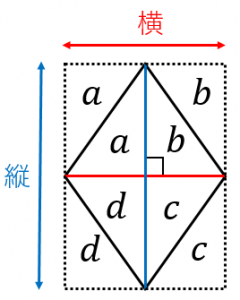
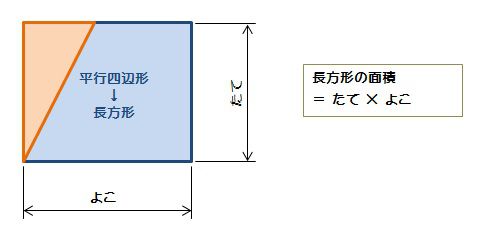
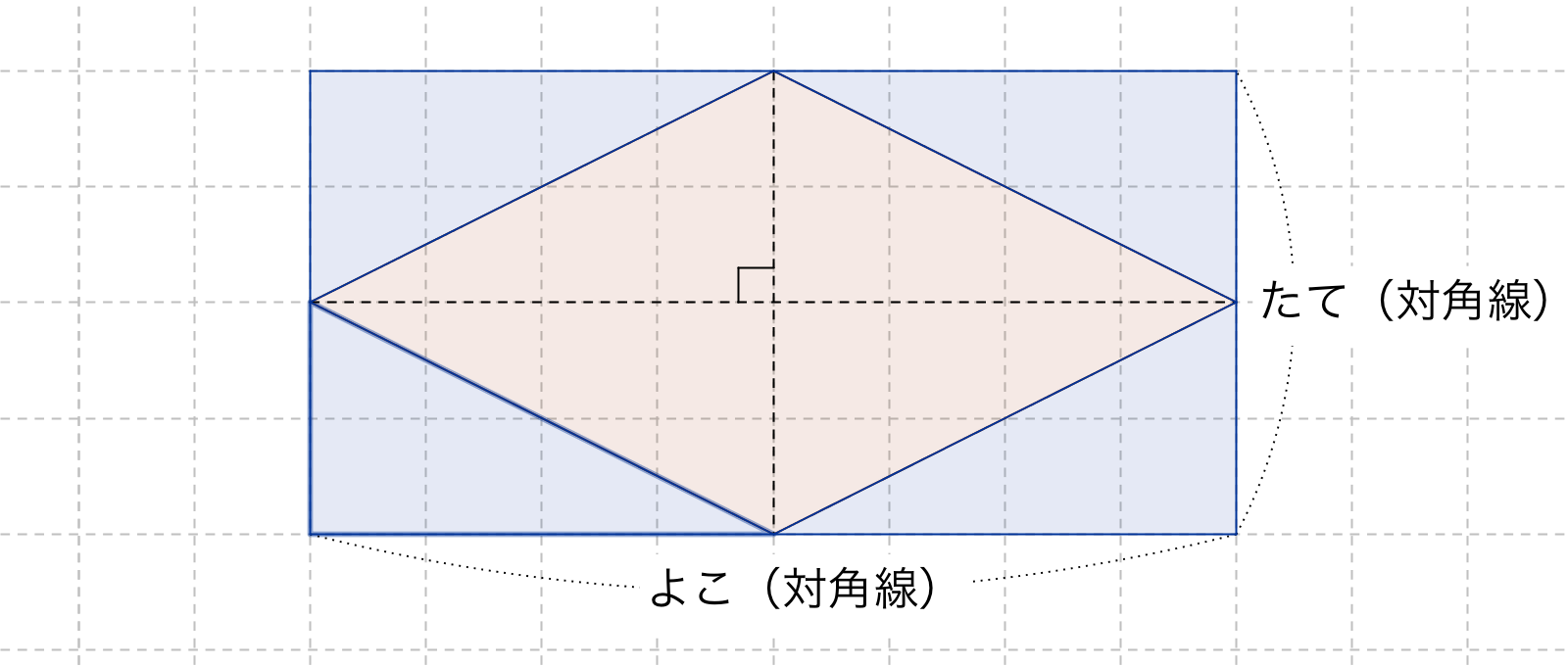
・台形の面積 上底と下底、高さから台形の面積を公式を使って計算します。 ・ひし形の面積 対角線の長さからひし形の面積を計算します。 ・平行四辺形の面積(底辺と高さ) 底辺と高さから平行四辺形の面積を計算します。三角形や平行四辺形の面積の公式を使って、ひし形の面積を工夫して求め、公式を導き出すことができる。 数学的な考え方 2 主な算数的活動について 表現する活動として、自力解決の場面で、実際に切ったり動かしたりするなどの作業的な活動を通して、面積を求める方法を考えさせる。 そして、自分なりに考えた方法を、単に式だけで表すのではなく、図 (ひし形abcdの面積 )=(長方形efca) = (長方形efgh)÷2 = (対角線)×(対角線)÷2 になるんだ。 底辺と高さをつかった菱形の面積の公式 つぎは、「底辺」と「高さ」をつかった公式だよ。 菱形の面積は、 (底辺)×(高さ) で計算できちゃうんだ。



平行四辺形の面積の公式 算数の公式



1
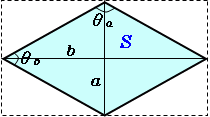
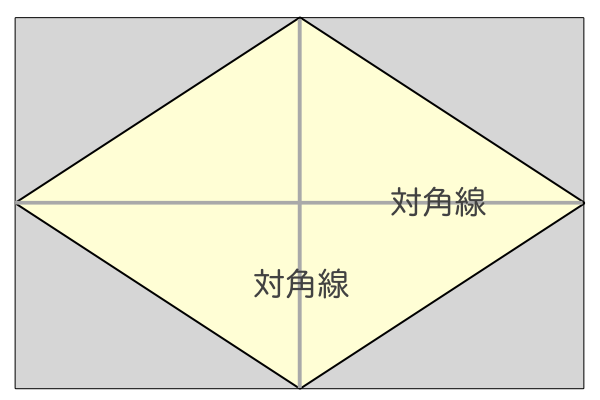
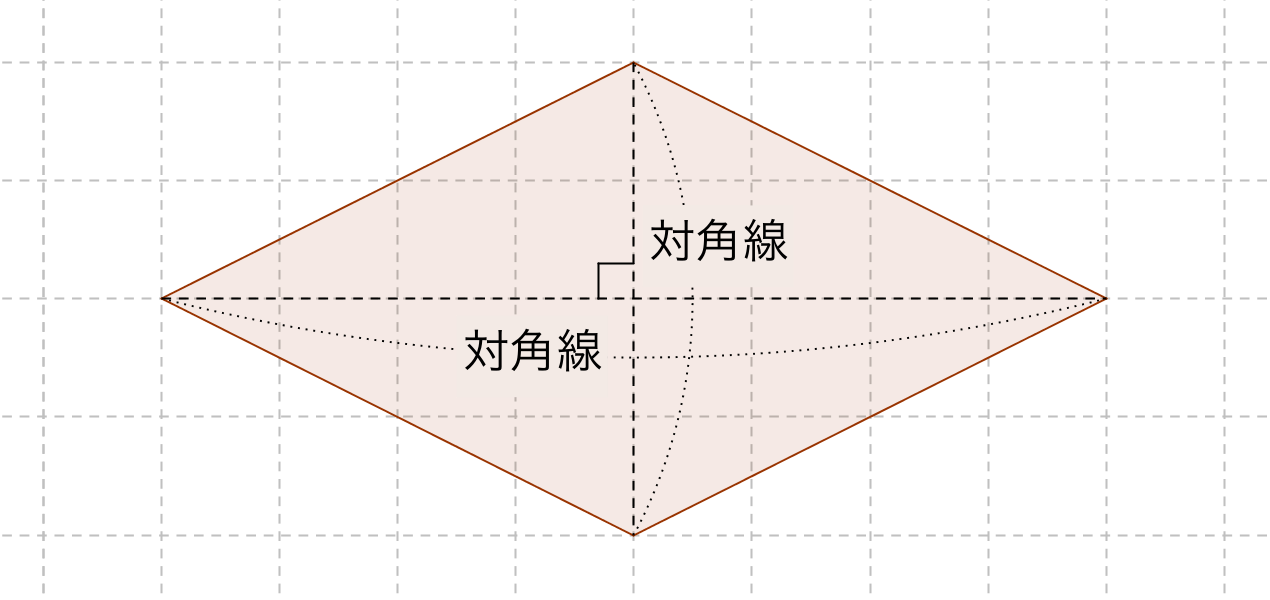
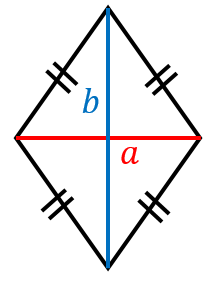
つまり、ひし形の面積は、対角線×対角線÷2ということが分かります。 まとめ ひし形の面積の求め方について解説しました。 ひし形の面積を求める公式は難しくありませんし、実際にこの公式を使うことができないという小学生は少数派です。2つの対角線の長さが $a$、$b$ のひし形の面積 $S$ は、次の公式で求められます。 ひし 形 (がた) の面積 \begin{align*} S = \frac{1}{2} ab \end{align*} 面積 = たての 対角線 (たいかくせん) × 横の対角 ひし形の面積の求め方公式 ひし形の面積を求めるときには次の公式を使います。 ひし形の面積=対角線×対角線÷2 (※対角線とは、ひし形の向かい合った頂点をそれぞれ直線で結んだもの) スポンサードリンク



ひし形の面積 簡単に計算できる電卓サイト




簡単公式 ひし形 菱形 の面積を計算できる2つの求め方 Qikeru 学びを楽しくわかりやすく
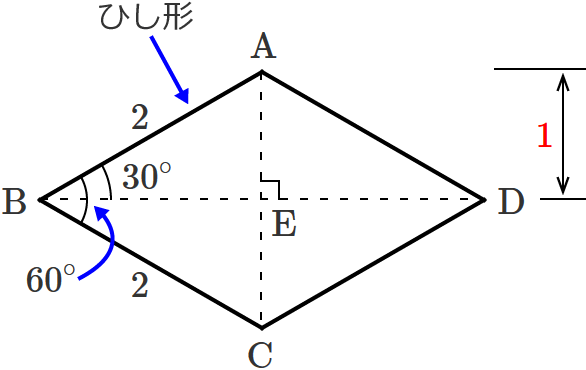
ひし形の面積の公式 ひし形の面積の求め方例題 ひし形の性質 性質①2 本の対角線は垂直に交わる 性質②2 本の対角線は、互いにほかを 2 等分する 性質③1 本の対角線は、ひし形を合同な 2 つの二等辺三角形に分けるア 三角形、平行四辺形、ひし形及び台形の面積の求め方を考えること。 〔算数的活動〕(1)イ 三角形、平行四辺形、ひし形及び台形の面積の求め方を、具体物を用いたり、 言葉、数、式、図を用いたりして考え、説明する活動 第4学年では、長方形と正方形の面積の学習において、1cm2 ひし形の面積2 今度は同じひし形の面積を、別の出し方で求めてみます。 A から BC に下した垂線の足を E とします。 BC を底辺、 AE を高さと考えて面積を出すこともできますね。 $\mathrm{ BC }=1$ であり、 $\mathrm{ AE }=\sin 2\theta$ なので、このひし形の面積は



ひし形の対角線の長さの求め方




小学5年算数 ひし形の面積 Youtube
ひし形の面積を求める公式は、s = (縦の対角線)×(横の対角線)÷2 で表されます。このページでは、ひし形の面積の求め方を、計算問題と共に説明しています。また、公式の導き方も説明しています。 たとえば、「4辺の長さがそれぞれ 5, 15, 8, 12 で1組の対角の和が 150 ° の四角形」の面積は、ブレートシュナイダーの公式を使うことで 30 30 3 ≒ 8196 と求まります。 ただし、 ∠ A と ∠ C の角度がそれぞれ分かっている場合は、 三角形の面積の公式 を5年算数面積 教え方のポイント ① 三角形 と 平行四辺形と台形・ひし形の面積 の求め方 ② 三角形 と 平行四辺形と台形・ひし形の面積 求め方の公式 ③ いろいろな三角形・四角形の面積の求め方 ④ 面積と比例の



小学算数の面積の求め方と公式一覧 四角形 長方形の性質や円の計算方法まで解説 学びtimes




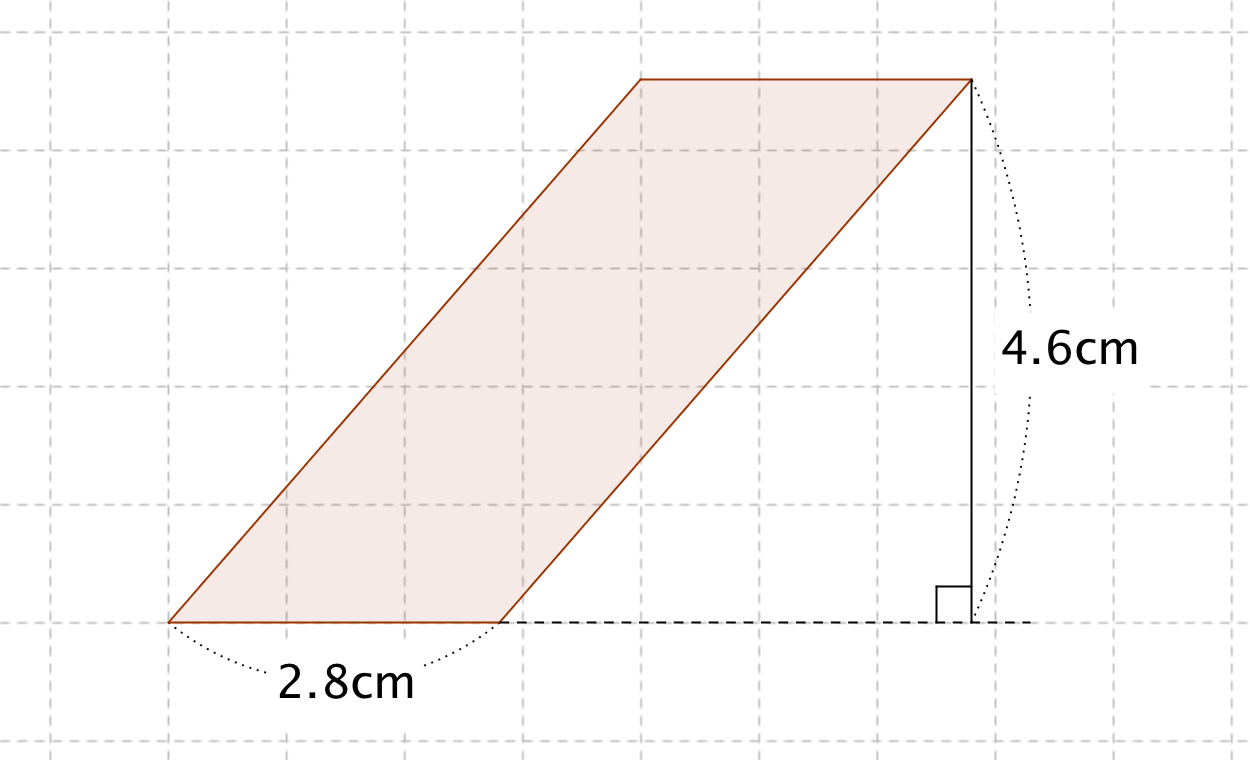
平行四辺形の面積の求め方 公式と計算例




ひし形の面積の求め方 公式と計算例



ひし形の対角線の長さの求め方



3分で分かる ひし形の面積の公式と問題の解き方をわかりやすく 合格サプリ



ひし形の面積の公式 Youtube




5年算数 面積 のわかる教え方 いっちに算数 のブログ




平行四辺形の面積の求め方 公式と計算例
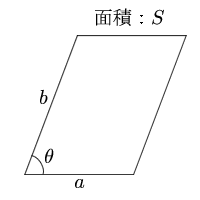



平行四辺形 2辺と間の角度 面積の計算 計算サイト




ひし形 の 面積 公式 小学校で習う 算数の公式一覧35種類 中学受験対策まとめ Docstest Mcna Net
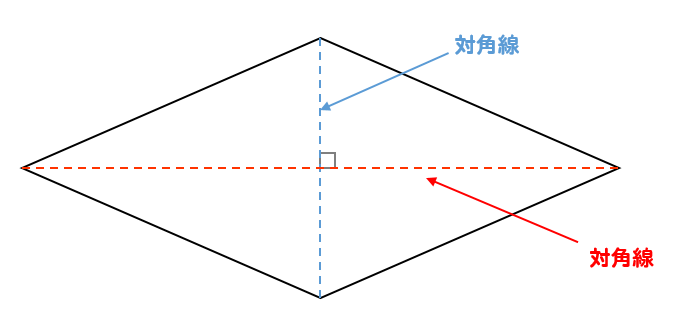



小学算数 ひし形の面積公式のなぜ 図を使って解説 数スタ




ひし形 菱形 の面積の公式は 対角線 対角線 2 見やすい図で即理解 高校生向け受験応援メディア 受験のミカタ




小5 算数 小5 41 平行四辺形の面積 Youtube




公式なんて覚えない ひし形の面積は直感的に考えよう
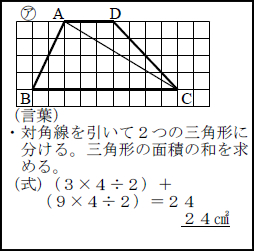



第5学年 面積 台形 私の実践 私の工夫アーカイブ一覧 授業支援 サポート資料 算数 小学校 知が啓く 教科書の啓林館




ひし形の面積 周りの長さを求める公式 小学生 中学生の勉強




ひし形の面積の求め方 公式と計算例
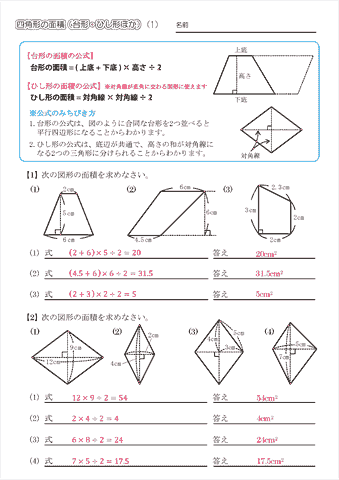



小学5年生の算数 四角形の面積 台形 ひし形ほか 問題プリント ちびむすドリル 小学生
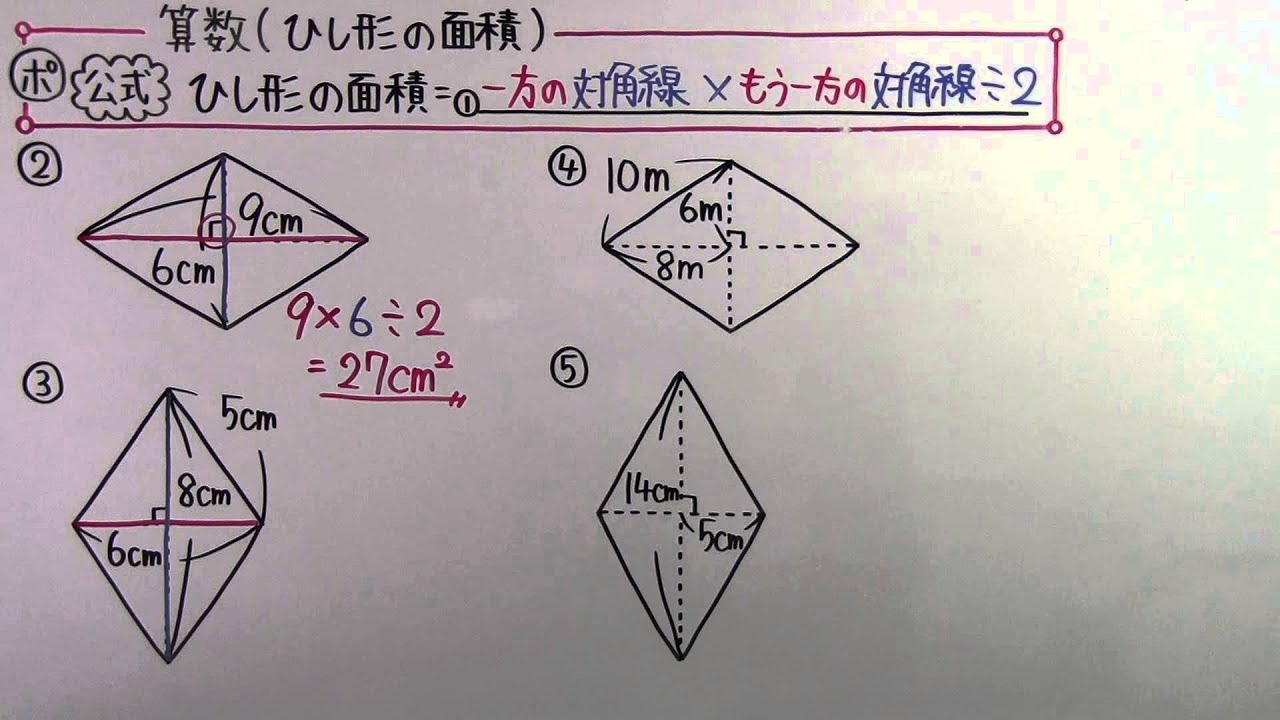



小5 算数 小5 44 ひし形の面積 Youtube




ひし形の面積の求め方 公式と計算例




ひし形の面積の公式 面積の求め方は対角線に注目しよう 中学や高校の数学の計算問題




小5 算数 小5 44 ひし形の面積 Youtube
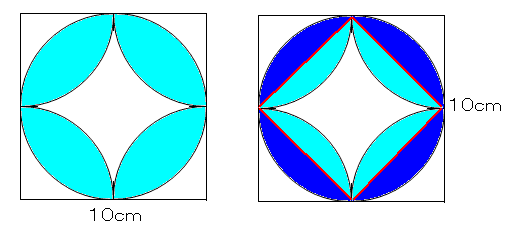



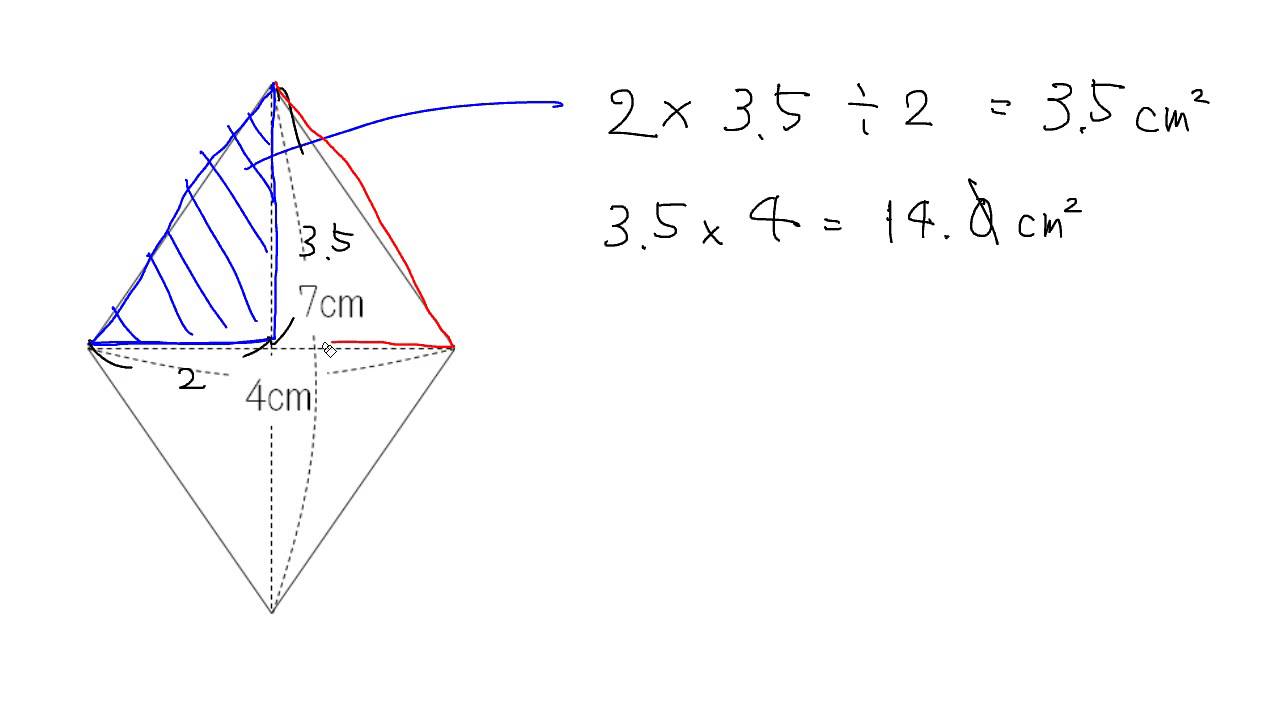
算数 扇形の面積の応用 葉っぱ型図形の面積 なるほどの素



1
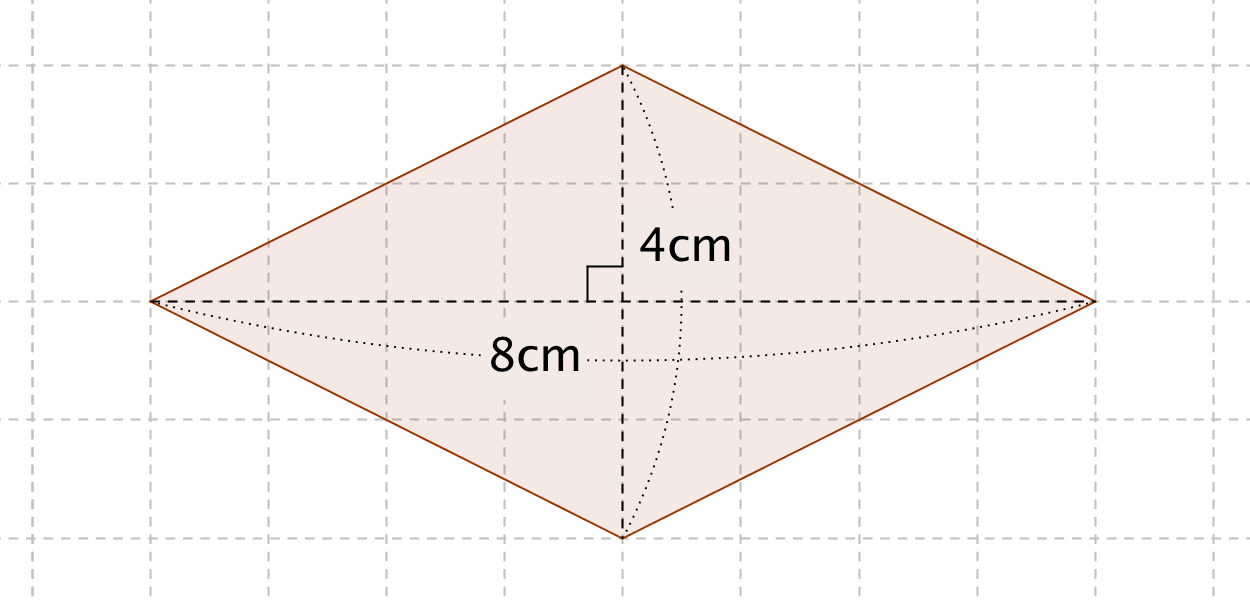



ひし形の面積の公式 算数の公式




5年算数面積 教え方のポイント




ひし形の面積の公式 小学生に教えるための分かりやすい解説 数学fun
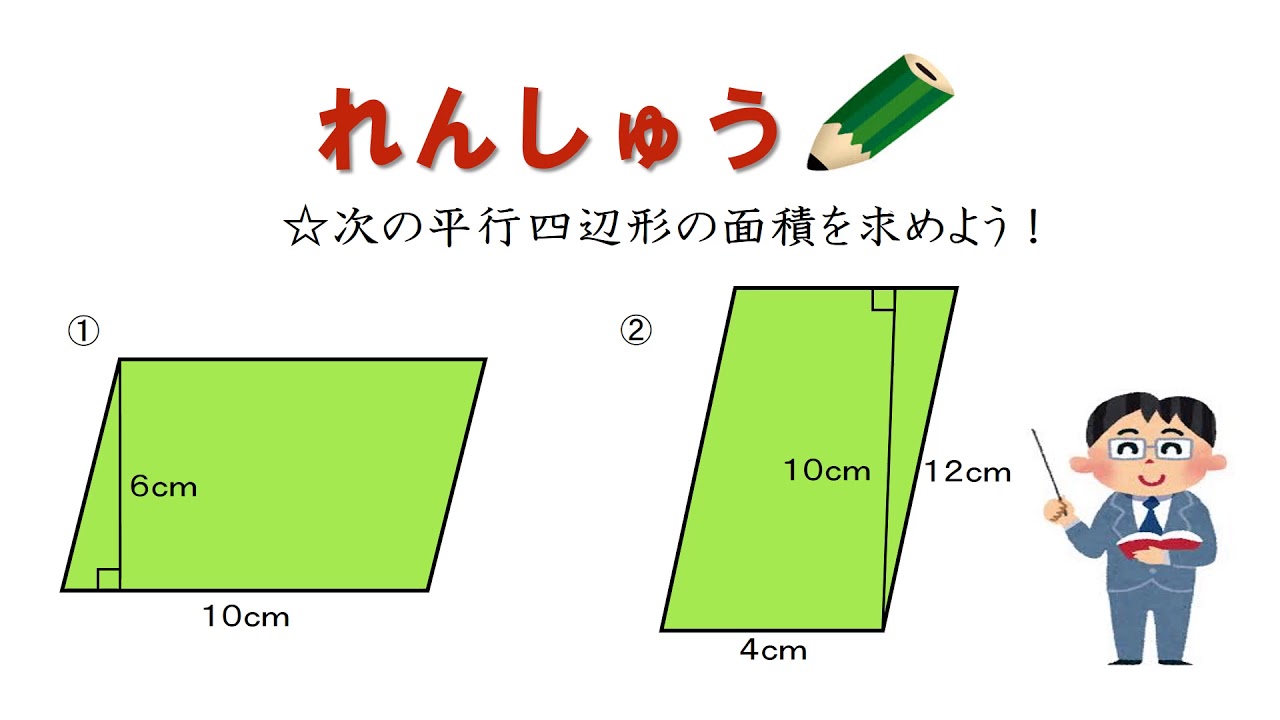



小5 面積の求め方を考えよう 平行四辺形の面積の求め方 日本語版 Youtube



なぜひし形の面積の求め方が 対角線 対角線 2分の1なのかを説明してくだ Yahoo 知恵袋




ひし形の面積 練習 Youtube




小学校で習うひし形の面積の求め方 対角線を使った公式で求められる理由 みけねこ小学校
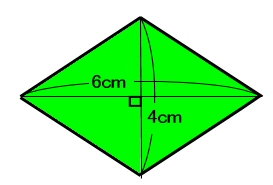



ひし形の面積の求め方



5年算数面積2 教え方のポイント
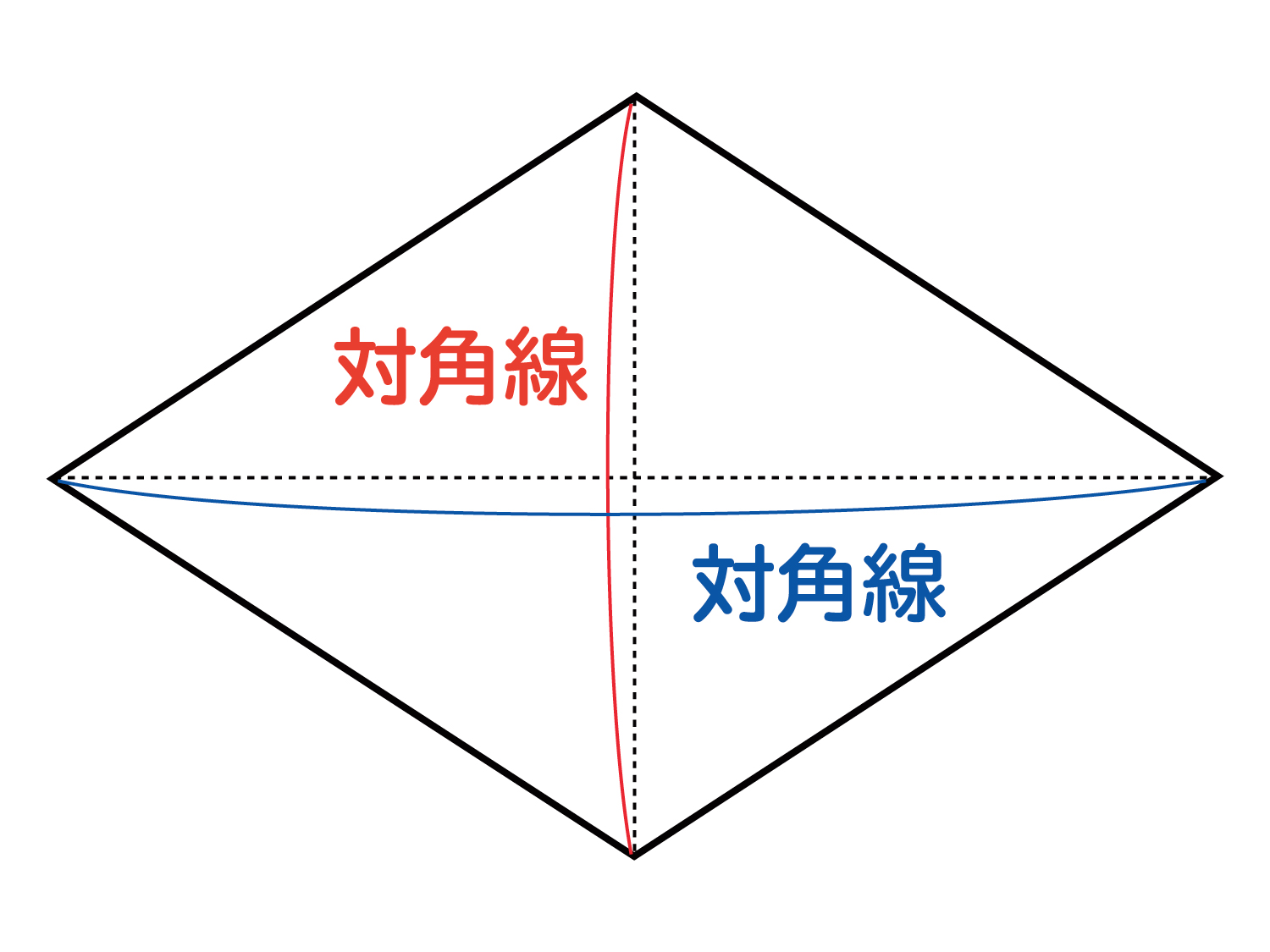



なぜ ひし形の面積は 対角線 対角線 2 なのか を説明します おかわりドリル
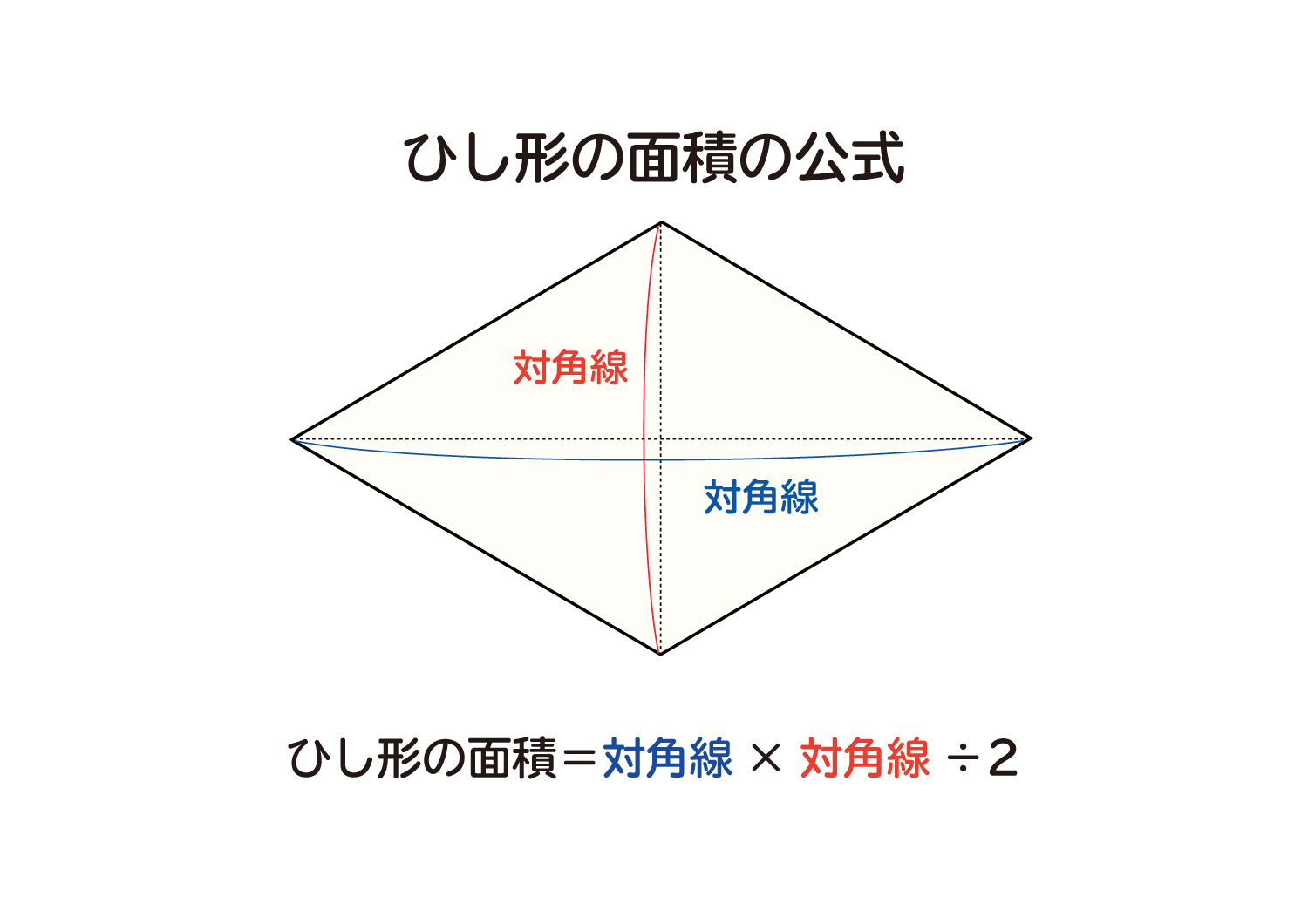



なぜ ひし形の面積は 対角線 対角線 2 なのか を説明します おかわりドリル




3分で分かる ひし形の面積の公式と問題の解き方をわかりやすく 合格サプリ
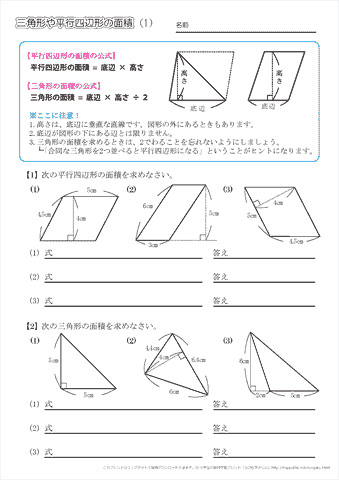



小学5年生の算数 三角形や平行四辺形の面積 問題プリント ちびむすドリル 小学生




四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ




簡単公式 ひし形 菱形 の面積を計算できる2つの求め方 Qikeru 学びを楽しくわかりやすく



平行四辺形の面積の公式 算数の公式



図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師




5年算数面積 教え方のポイント



お知らせ 中丹教育局



ひし形の面積を求める方法と例題 具体例で学ぶ数学




たこ形の面積の求め方を考えよう 5年算数 茎崎学園 つくば市立茎崎第二小学校



3
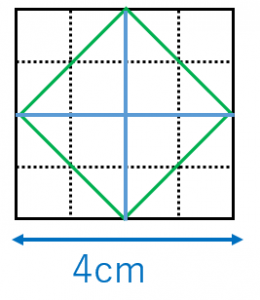



正方形の面積を求める2つの公式 具体例で学ぶ数学




台形の面積の求めかたは 忘れても大丈夫 公式は自分でつくろう




面積の求め方 算数の教え上手 学びの場 Com



ひし形の面積の公式 算数の公式



平行四辺形とひし形の違いってなに それぞれの特徴を比較 数スタ



平行四辺形の面積の公式 算数の公式




5年 ひし形の面積の求め方 Youtube




平行四辺形の面積の公式 なぜ 底辺 高さ で求められるのか 数学fun




正方形の面積を求める2つの公式 具体例で学ぶ数学



1




平行四辺形の面積の求め方 公式と計算例




簡単公式 ひし形 菱形 の面積を計算できる2つの求め方 Qikeru 学びを楽しくわかりやすく




ひし形の面積 周りの長さを求める公式 小学生 中学生の勉強



算数道場 4 面積と体積 1 面積の意味と単位 その9 ひし形の面積



平行四辺形の面積 算数の公式覚えてますか




面積8 12の流れ



なぜ 台形の面積は 上底 下底 高さ 2 なのか を説明します おかわりドリル
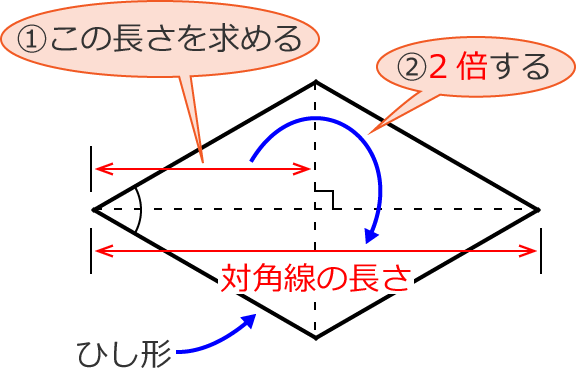



ひし形の対角線の長さの求め方



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典




小学5年生 ひし形 台形の面積 算数 Active Learning 学院




ひし形の面積の求め方 公式と計算例




簡単公式 ひし形 菱形 の面積を計算できる2つの求め方 Qikeru 学びを楽しくわかりやすく



ひし形の面積の公式 算数の公式
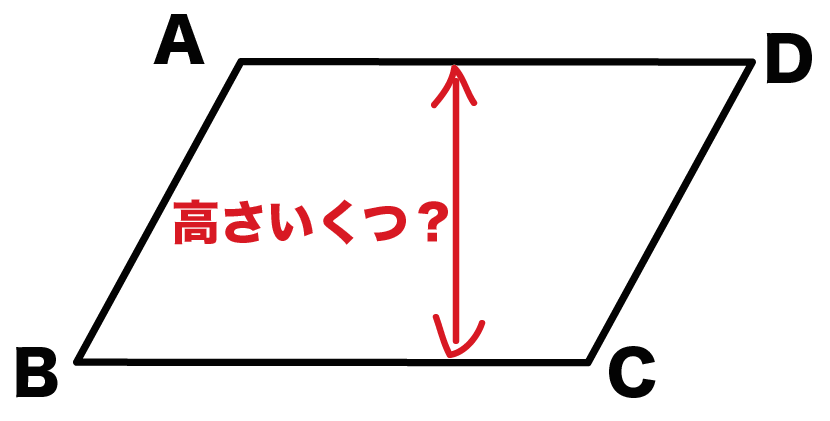



中学数学 平行四辺形の高さの2つの求め方 Qikeru 学びを楽しくわかりやすく




平行四辺形の面積の求め方 公式 小学生 中学生の勉強




簡単公式 ひし形 菱形 の面積を計算できる2つの求め方 Qikeru 学びを楽しくわかりやすく




簡単公式 ひし形 菱形 の面積を計算できる2つの求め方 Qikeru 学びを楽しくわかりやすく




すきるまドリル 小学5年生 算数 図形の面積 無料学習プリント すきるまドリル 無料学習プリント




関数 グラフ上の平行四辺形の座標 面積 二等分線などの問題を解説 数スタ



ひし形 菱形 とは 定義や面積の求め方 公式 計算問題 受験辞典



Www Wakayama Wky Ed Jp Nagusa Wp Content Uploads Sites 52 18 03 Afa4f4ae2913a9c5643adc5 1 Pdf




四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ




平行四辺形の面積の求め方 公式と計算例




簡単公式 ひし形 菱形 の面積を計算できる2つの求め方 Qikeru 学びを楽しくわかりやすく




台形の面積の公式 小学生に教えるための分かりやすい解説 数学fun



3分で分かる ひし形の面積の公式と問題の解き方をわかりやすく 合格サプリ




平行四辺形の面積の求め方 公式と計算例




面積 台形 ひし形の面積 01 ひし形の面積 Youtube




平行四辺形の対角線の長さの求め方




簡単公式 ひし形 菱形 の面積を計算できる2つの求め方 Qikeru 学びを楽しくわかりやすく



ひし形の面積を求める方法と例題 具体例で学ぶ数学




平行四辺形の面積を求める公式 あまり知られていないかも 中学や高校の数学の計算問題



ひし形の面積は 1分でわかる求め方 公式 辺の長さ 対角線との関係



5年算数面積2 教え方のポイント




小学5年生の算数 四角形の面積 台形 ひし形ほか 問題プリント ちびむすドリル 小学生



三角形の面積公式 小学生はどうやって解く 問題を使って解説 数スタ



0 件のコメント:
コメントを投稿