Just two points are needed to draw a straight line graph, although it is a good idea to do a check with another point once you have drawn the graph Example Draw the graph of \(y = 3x 1\)Thus, to graph an equation in two variables, we graph the set of ordered pairs that are solutions to the equation For example, we can find some solutions to the firstdegree equation y = x 2 by letting x equal 0, 3, 2, and 3 Then, for x = 0, y=02=2 for x = 0, y = 3 2 = 1 for x = 2, y =TITLE 'Average Monthly Rainfall in Olympic Cities';

X And Y Graph Definition Differences Equation On X And Y Graph Examples
Example of x y graph
Example of x y graph-Excel Plot X vs Y We will set up a data table in Column A and B and then using the Scatter chart;Example 4 Graph x y Solution First graph x = y Next check a point not on the line Notice that the graph of the line contains the point (0,0), so we cannot use it as a checkpoint To determine which halfplane is the solution set use any point that is obviously not on the line x = y The point ( 2,3) is such a point




Example The Graph Of X Y 2 Shown Below Is Symmetric To X Axis Y X 1 2 323 A Graph Is Symmetric To X Axis If Whenever X Y Is On Graph So Ppt Download
Plot (X,Y) creates a 2D line plot of the data in Y versus the corresponding values in X If X and Y are both vectors, then they must have equal length The plot function plots Y versus X If X and Y are both matrices, then they must have equal size The plot function plots columns of Y versus columns of XGraph the linear function f(x) = − 5 3x 6 and label the x intercept Solution From the function, we see that f(0) = 6 (or b = 6) and thus the y intercept is (0, 6) Also, we can see that the slope m = − 5 3 = − 5 3 = rise run Starting from the y intercept, markThe graph of f x = x − a b can be obtained by translating the graph of f x = x to a units to the right and then b units up Example Sketch the graph of y = x − 1 2 from its parent graph y = x
Y=x^21 (Graph Example), 4x2=2 (x6) (Solve Example) Algebra Calculator is a calculator that gives stepbystep help on algebra problems See More Examples » x3=5 1/3 1/4 y=x^21 Disclaimer This calculator is not perfect Please use at your own risk, and please alert us if something isn't working Thank youAn example of a discontinuous graph is y = 1/x, since the graph cannot be drawn without taking your pencil off the paper A function is periodic if its graph repeats itself at regular intervals, this interval being known as the period A function is even if it is unchanged when x is replaced by x The graph of such a function will be symmetrical in the yaxisExample 5 use a cubic graph to solve the equation Use the graph of y = x^3 5x 1 to find an approximate solution of the following equation \x^35x1=6\ Find the given value on the yaxis The value of 6 is in place of the y We need to look on the yaxis for the value of 6
Again, this graph has the line y = 0 as an asymptote Variations on the General Graph Note that if b is negative, the curve will curve downward as the x values increase Note that if the exponent is negative, the curve will tend upward in the negative x values Consider these basic forms for y = −2 x and y = 2 −x respectivelyFunctions & Graphing Calculator \square!An element x of X is a direct predecessor of an element y of X if and only if xRy A directed graph can model information networks such as Twitter, with one user following another Particularly regular examples of directed graphs are given by the Cayley graphs of finitelygenerated groups, as well as Schreier coset graphs




Graph Of Y X And Y F X In Example 9 Download Scientific Diagram
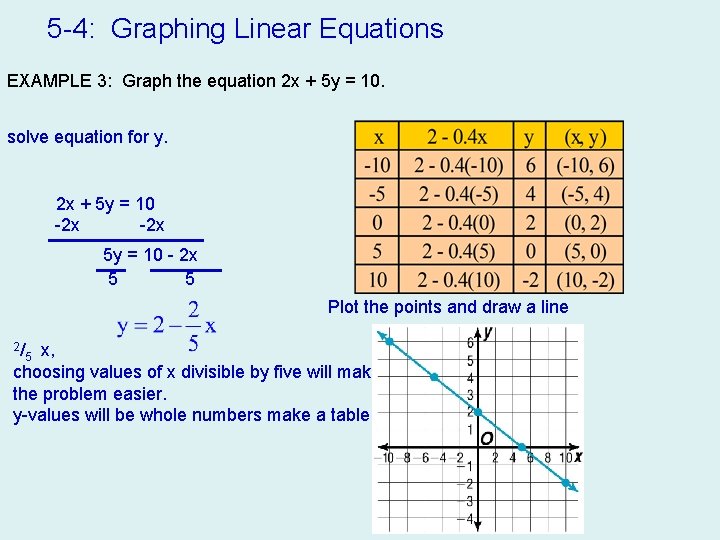



Graph The Linear Equation Yx 2 1 Draw
An example XY Chart, showing one set of numerical data along the xaxis and another along the yaxis The following example XY Chart combines values into single data points and displays them in uneven intervals, or clusters XY Chart is often used for analyzing engineering, scientific and statistical data When two or more values are compared, it is easy to measure the performance of Find the vertical asymptote, the horizontal asymptote, and the lines of symmetry for the reciprocal function y= 1 / x 5 Then, graph the function Example 2 Solution As before, we can compare the given function to the parent function y= 1 / x In this case, the only difference is that there is a 5 at the end of the function, signifying a vertical shift upwards by five unitsPlot (x2,y) The way x2 is defined above, it is a vector of numbers between pi and pi with an increment of 1 You may need to experiment with this increment depending on what your curve is to get a smooth graph but without too many elements in the vector so the computer isn't unnecessarily slow



How Do You Graph The Line Y X 2 Example
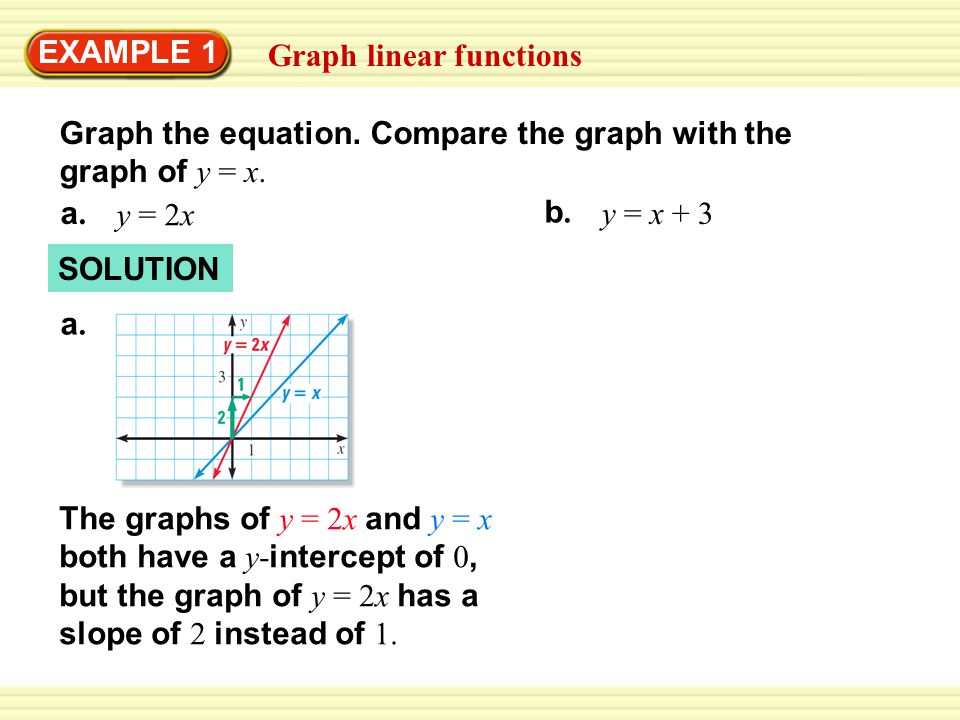



Graph Linear Functions Example 1 Graph The Equation Compare The Graph With The Graph Of Y X A A Y 2x B B Y X 3 Solution A A The Graphs Of Ppt Download
Question (x, y) (x, y) (x, y) Example Graph triangle ABC with vertices A(2, 1), B(3, 8) and C(7, 2) and its image after a 90° counterclockwise rotation about the origin Example Graph triangle XYZ with vertices X(5, 1), 7(7, 6) and 21, 2) and its image after a 180° rotation about the originThe asymptote of y = f (x) y=f(x) y = f (x) is the x x xaxis f (x) f(x) f (x) is a decreasing function Therefore, the graph of y = − a x (a > 1) \displaystyle y=a^x~(a>1) y = − a x (a > 1) is (E) (E) \ _\square (E) If the graph below represents y = 3 x, y=3^x, y = 3 x, what is b − a?How To Given an exponential function with the form latexf\left(x\right)={b}^{xc}d/latex, graph the translation Draw the horizontal asymptote y = d Shift the graph of latexf\left(x\right)={b}^{x}/latex left c units if c is positive and right latexc/latex units if



Y



Quadratics Graphing Parabolas Sparknotes
Example 1 Graph the equation of the line 2 x − 4 y = 8 2x4y=8 2x − 4y = 8 using its intercepts I hope you recognize that this is an equation of a line in Standard Form where both the x and y variables are found on one side of the equation opposite the constant termFor example, the black dots on the graph in the graph below tell us that f (0) = 2 f ( 0) = 2 and f (6) = 1 f ( 6) = 1 However, the set of all points (x,y) ( x, y) satisfying y =f (x) y = f ( x) is a curve The curve shown includes (0,2) ( 0, 2) and (6,1) ( 6, 1) because the curve passes through those pointsThe yintercept of a graph is (are) the point(s) where the graph intersects the yaxisWe know that the xcoordinate of any point on the yaxis is 0So the xcoordinate of a yintercept is 0 Here is an example of a yinterceptConsider the line y = x 3 This graph meets the yaxis at the point (0,3) Thus (0,3) is the yintercept of the line y = x 3




Graph Y X 2 Study Com
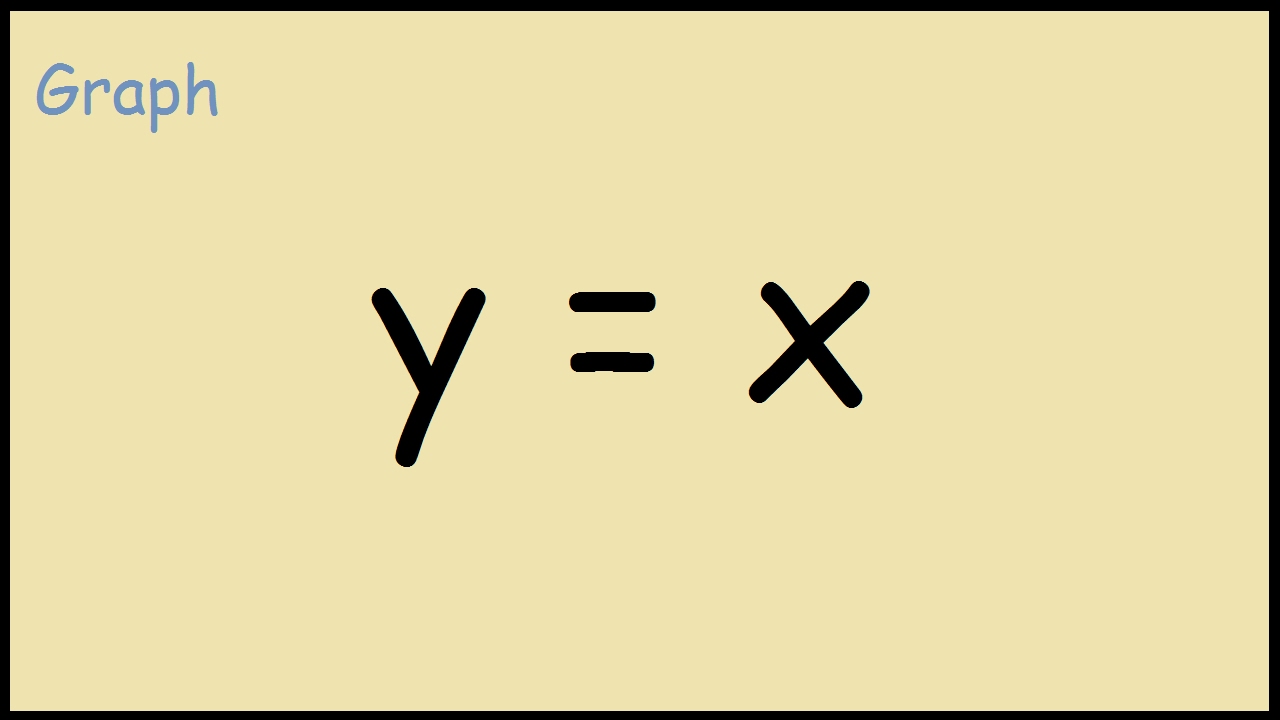



How To Graph The Line Y X Youtube
We will display, modify, and format our X and Y plots We will set up our data table as displayed below Figure 2 – Plotting in excel Next, we will highlight our data and go to the Insert Tab Figure 3 – X vs Y graph in ExcelVideo presentation of this example — Graphing \(y=x^26 x\) as an example of \(y = a x^2 b x c\) over the domain \(10 \le x \le 10\text{}\) For the second example, we want the same graph, but we want the ability to easily convert the graph of ourEvery point (x, y) is the same distance r from the center Therefore, according to the Pythagorean distance formula for the distance of a point from the origin x 2 y 2 = r 2 This is the equation of a circle of radius r, with center at the origin (0, 0) Specifically, this x 2 y 2 = 25 is the equation of a circle of radius 5 centered at the origin
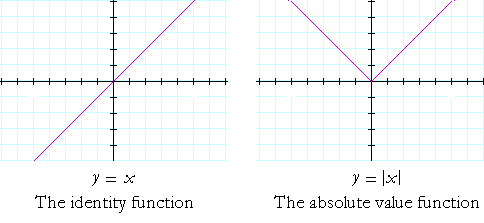



Graph Of A Parabola Topics In Precalculus




Example The Graph Of X Y 2 Shown Below Is Symmetric To X Axis Y X 1 2 323 A Graph Is Symmetric To X Axis If Whenever X Y Is On Graph So Ppt Download
Example 2y − x ≤ 6 1 We will need to rearrange this one so "y" is on its own on the left Start with 2y − x ≤ 6 Add x to both sides 2y ≤ x 6 Divide all by 2 y ≤ x/2 3 2 Now plot y = x/2 3 (as a solid line because y≤ includes equal to) 3Note that this type of curve, the graphs of y = where k is a real number and x ≠ 0, has two lines of symmetry y = x and y = x How To Graph Reciprocal Functions By Plotting Points?Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!



How Do You Graph The Line Y X 2 Example
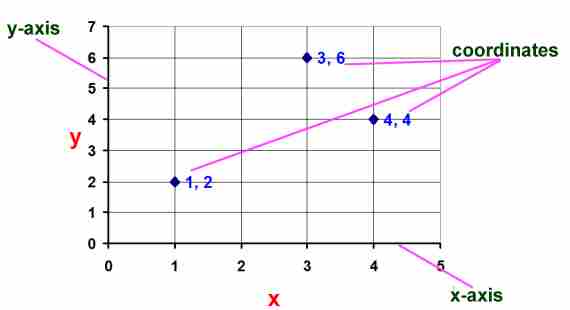



Kids Math Graphs And Lines Glossary And Terms
Graph of y = x 1Slope = 1Gradiant = Rise/Run = 1/1 = 1 (Run is always 1)We have a line with slope of 1 and intercepts the yaxis at 1 with two points weFor example, let fx()= x3 and gx()= x5 Compare the graphs of f and g Based on our experience from Part F, we expect that theHere's a better way x2=pi1pi;




Linear Graphs Xcelerate Math



X And Y Graph Definition Differences Equation On X And Y Graph Examples
Example Find the coordinates of the x and yintercepts of the graph of y = 2x 6 Plug y = 0 into y = 2x 6 0 = 2x 66 = 2x x = 3 The xintercept is located at (3, 0) Plug x = 0 into the equation y = 2 × 0 6 y = 6 The yintercept is located at (0, 6)On the x and y graph, a linear equation can be graphed showing the coordinates of both the xaxis and yaxis In geometry, a linear equation can be graphed by using the x and y graph and it is represented as a straight line Let us look at an example to understand this better Let's consider a linear equation y = 2x 1 Now to graph thisExample 1 The graph of y = 3 4 x − 2 has its y intercept at − 2 Similarly, for a quadratic equation written in standard form y = a x 2 b x c , the y intercept is c Example 2 The graph of y = − x 2 − x 3 has its y intercept at 3



Logarithmic And Exponential Graphs
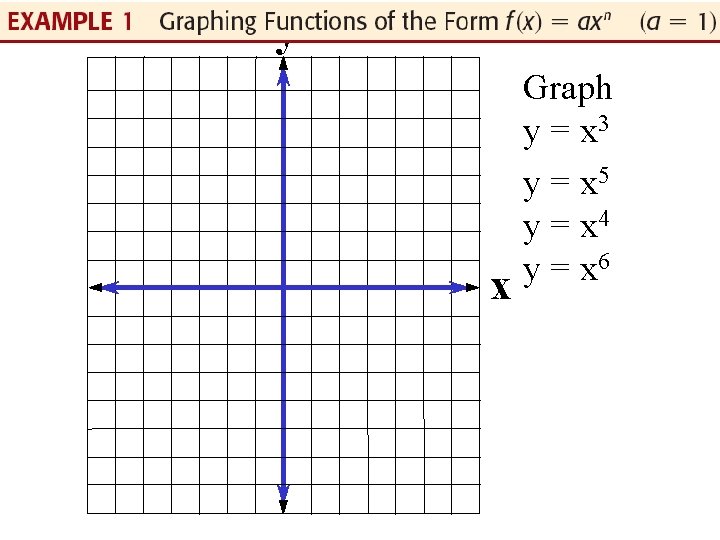



Chapter 3 4 Polynomial Functions Y X Graph
SERIES X = Month Y = BRain;Example 1 Graph the point (4, 3) The first number in the parentheses, aka the x value, is 4 This is how far we go horizontally, on the x axis, from (0, 0) Because it's negative, we go left We don't put a point there yet, though We still need to moveExample The diagram shows a graph of y = sin x for 0˚ ≤ x ≤ 360˚, determine the values of p, q and r Solution In order to answer this type of questions, you will need to remember the general properties (or shape) of a sine graph We know that the maximum value of a sine graph




Solved 1 Y X 8x2 5x 3 A Graph Y Be Sure To Label Chegg Com
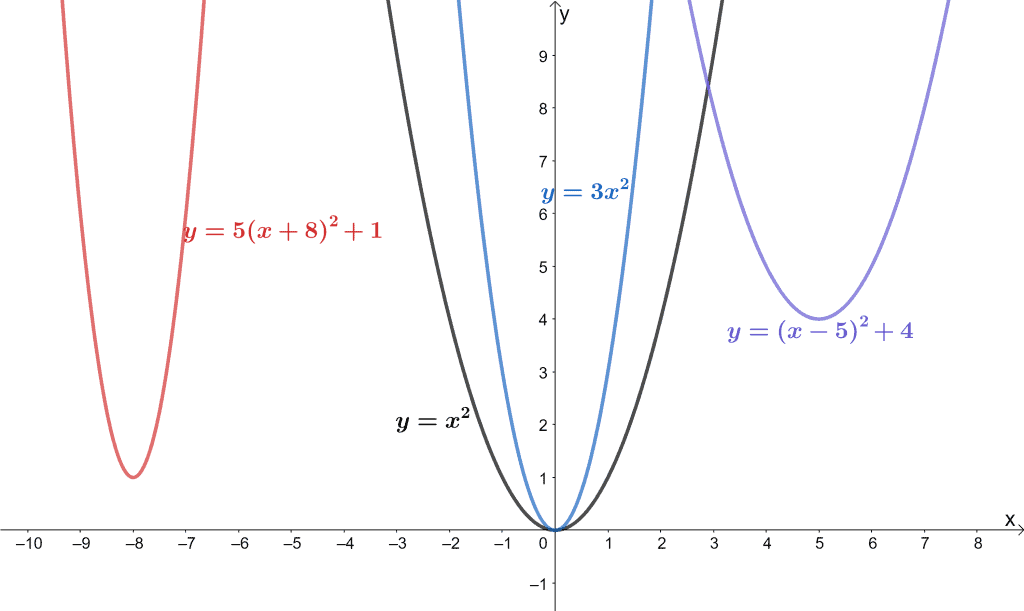



Parent Functions Types Properties Examples
In straight line graphs it is better to determine 3 points as the third point acts as a check They should all line up Mark the points and draw a straight line through extending it to the edge of the squared area on the paper For example Graph of y = x −3 This gets you extra marks You must label your axis as well!Answer (1 of 3) Just take two values of x and find the corresponding values of y Then plot the graph Example Given, y =x/4 Taking x = 0 is the easiest thing which we can do So if x = 0, y = 0/4 = 0 Next let's take x = 4 which gives y = 4/4 = 1 So we have the points (0,0) and (4,1) Plot• The graphs of y = x 5, y = x7, etc resemble the graph of y = x3 • In Part C, we saw that the graph of y = x is a line • We will discuss the cases with negative exponents later How do these graphs compare?




Solved 3 What Transformation Must You Apply To The Graph Of Y X 2 In Order To Draw The Graph Of Y X 3 2 Note Represents Exponent For Example X 2




Online Tutoring Math English Science Tutoring Sat Psat Gmat Toefl Ielts Tutors Homework Help
EMBELLISHING GRAPHS So far the examples have shown how to create basic graphs The remaining examples show statements and options you can use to change the appearance of your graphs XAXIS AND YAXIS STATEMENTSBelow are graphs of some examples of functions of two variables On the left is a graph of the function z=x^2y^2 and on the right is a graph of the function z=sin(sqrt(x^2y^2)) It is difficult to completely represent a function of more than 2 variables graphically, since for a function of n variables, n1 dimensional space is required The equation #y=x# is saying whatever value you decide to give to #x# will also end up being the same value for #y# Notice that the graph goes upwards as you move from left to right This is called a positive slope (gradient) If it had been #y=x# then the slope would go down as you move from left to right This is what happens when the #x# in the equation is written as #x#
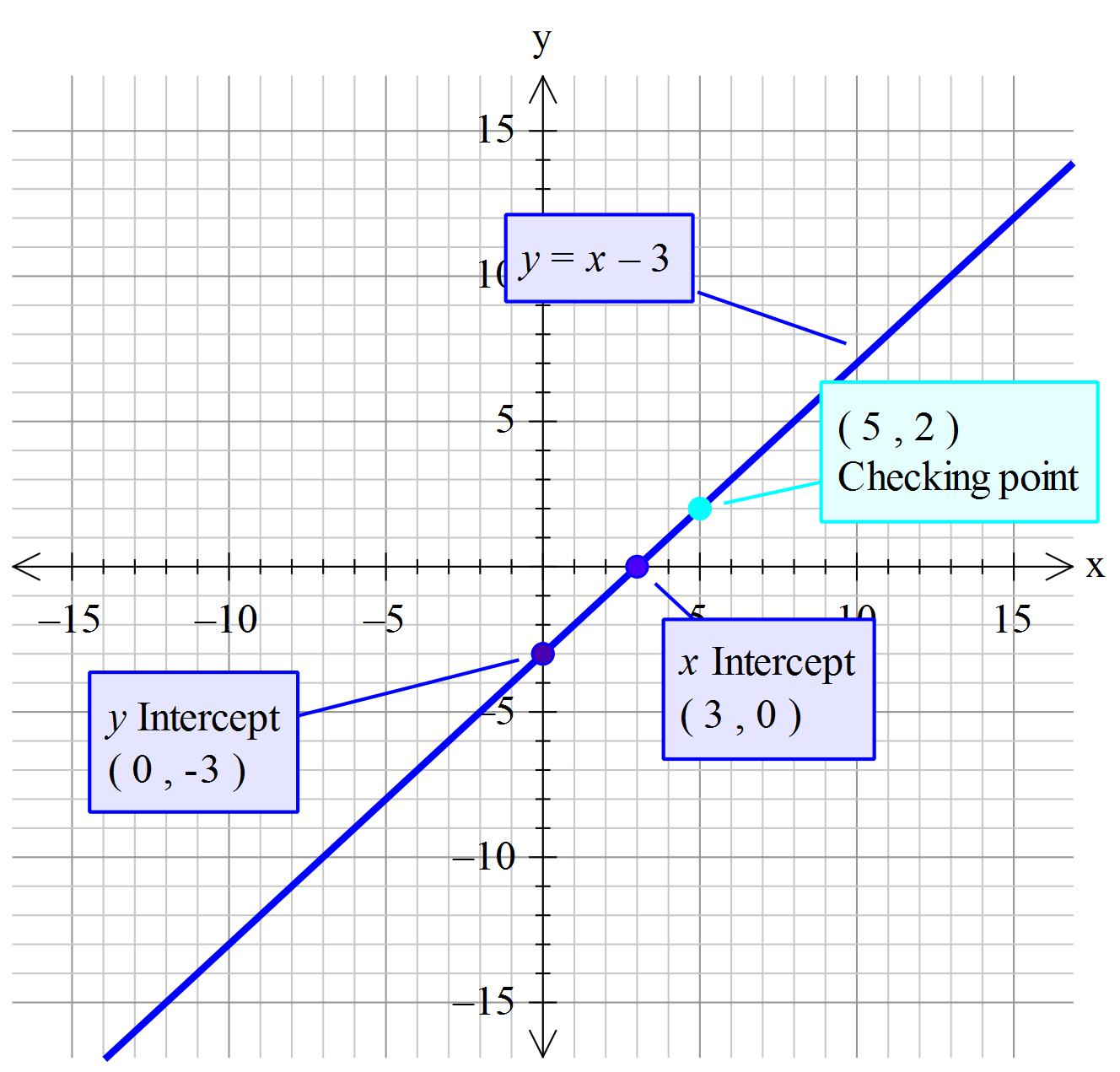



How Do You Graph Y X 3 Example



Matlab Plotting
In the parent function, the yintercept and the vertex are one and the same In the function (x1) 3, the yintercept is (01) 3 =(1) 3 =1 The xintercepts Unlike quadratic functions, cubic functions will always have at least one real solution They can have up to three For example, the function x(x1)(x1) simplifies to x 3x From the initial form of the function, however, we can see that this function will be equal to 0 when x=0, x=1, or xAlgebra Examples Popular Problems Algebra Graph y=x y = −x y = x Use the slopeintercept form to find the slope and yintercept Tap for more steps The slopeintercept form is y = m x b y = m x b, where m m is the slope and b b is the yintercept y = m x b y = m x bY − y 1 = m(x − x 1) y − 180 = 33(x − 12) y = 33(x − 12) 180 y = 33x − 396 180 y = 33x − 216 INTERpolating Now we can use that equation to interpolate a sales value at 21° y = 33×21 ° − 216 = $477 EXTRApolating And to extrapolate a sales value at 29° y = 33×29° − 216 = $741 The values are close to what we got on the graph




Slope Intercept Form Graphing Lines Free Math Help
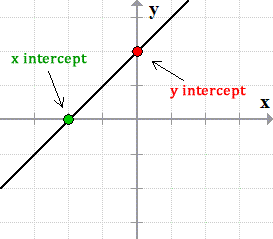



Graph A Line Using X And Y Intercepts Chilimath
Clickable Demo Try entering y=2x1 into the text box After you enter the expression, Algebra Calculator will graph the equation y=2x1 Here are more examples of how to graph equations in Algebra Calculator Feel free to try them now Graph y=x^22x y=x^22x Graph y= (x3)^2 y= (x We can see even more detail for small values of x and y now, however we can't include the negative temperatures on the horizontal axis Example 4 Variable Raised to a Fractional Exponent Graph y = x 1/2 using all 4 axis types (rectangular, both types of semilog, and loglog) This function is equivalent to `y=sqrt(x)` AnswerFree graphing calculator instantly graphs your math problems



Y




Graphs And Level Curves
SERIES X = Month Y = VRain;SERIES X = Month Y = LRain;The graph of a function f(x,y) with domain D is a collection of points (x,y,z) in space such that z = f(x,y), (x,y) ∈ D The domain D is a set of points in the xy plane The graph is then obtained by moving each point of D parallel to the z axis by an amount equal to the corresponding value of the function z = f(x,y) If D is a
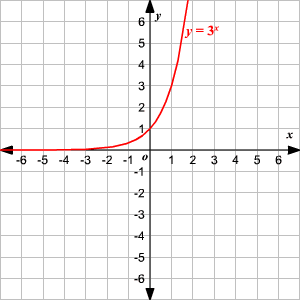



Graphing Logarithmic Functions




Graphs Types Examples Functions Video Lesson Transcript Study Com
Example Draw the graph of y = for values between 4 and 4, except for x = 0 Solution



1
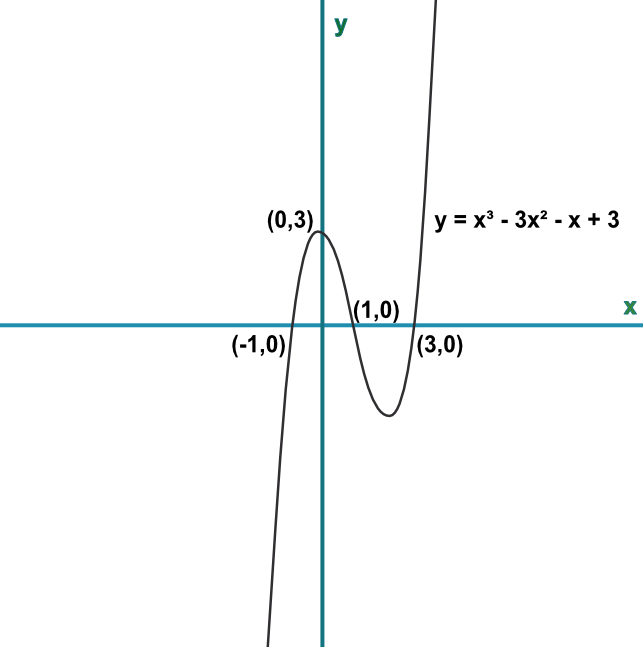



Graphing Cubic Functions
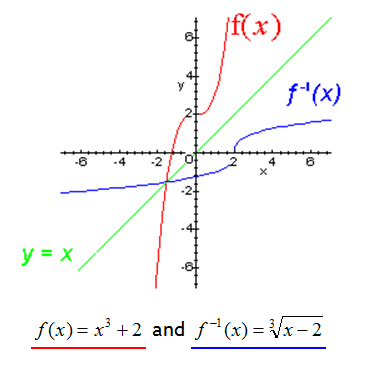



Inverse Functions Example 1




Intercepts Of Lines Review X Intercepts And Y Intercepts Article Khan Academy




9 Example 2 2 Next We Study The Function Y X 2 1 In The Real Plane Download Scientific Diagram




Example 4 Graph A Translated Square Root Function Graph Y 2 X 3 2 Then State The Domain And Range Solution Step Graphing Quadratics Function Of Roots



Solution Graph The Line Y X 3




Equation Xy Yx Wikipedia




How To Graph The Line Y X Youtube
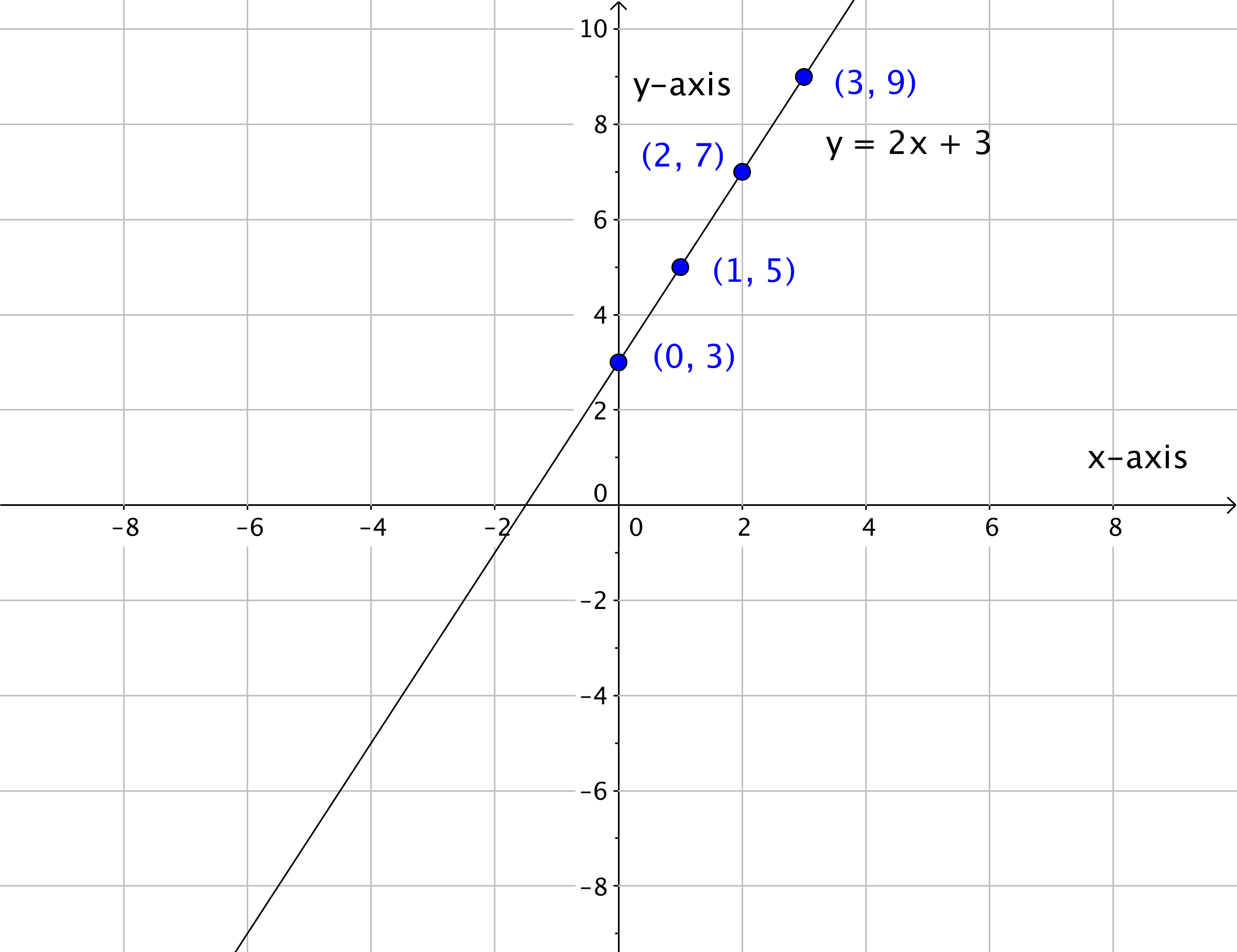



1 3 Coordinate Plane And Graphing Equations Hunter College Math101
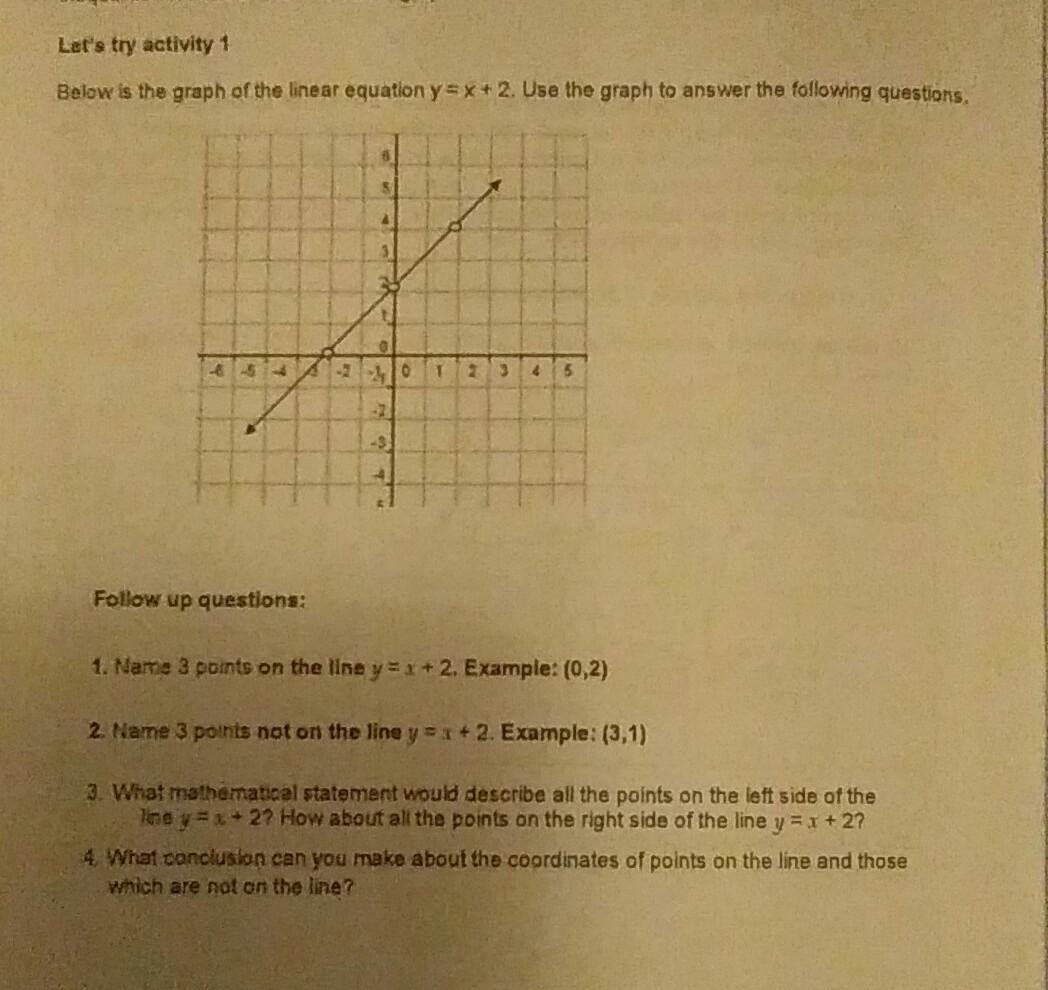



Solved Let S Try Activity 1 Below Is The Graph Of The Linear Chegg Com
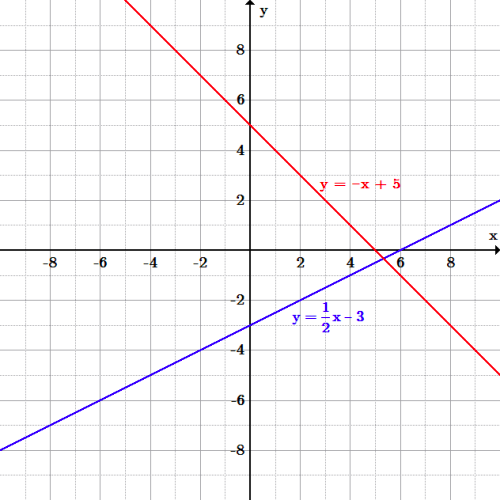



Introduction To Linear Functions Boundless Algebra
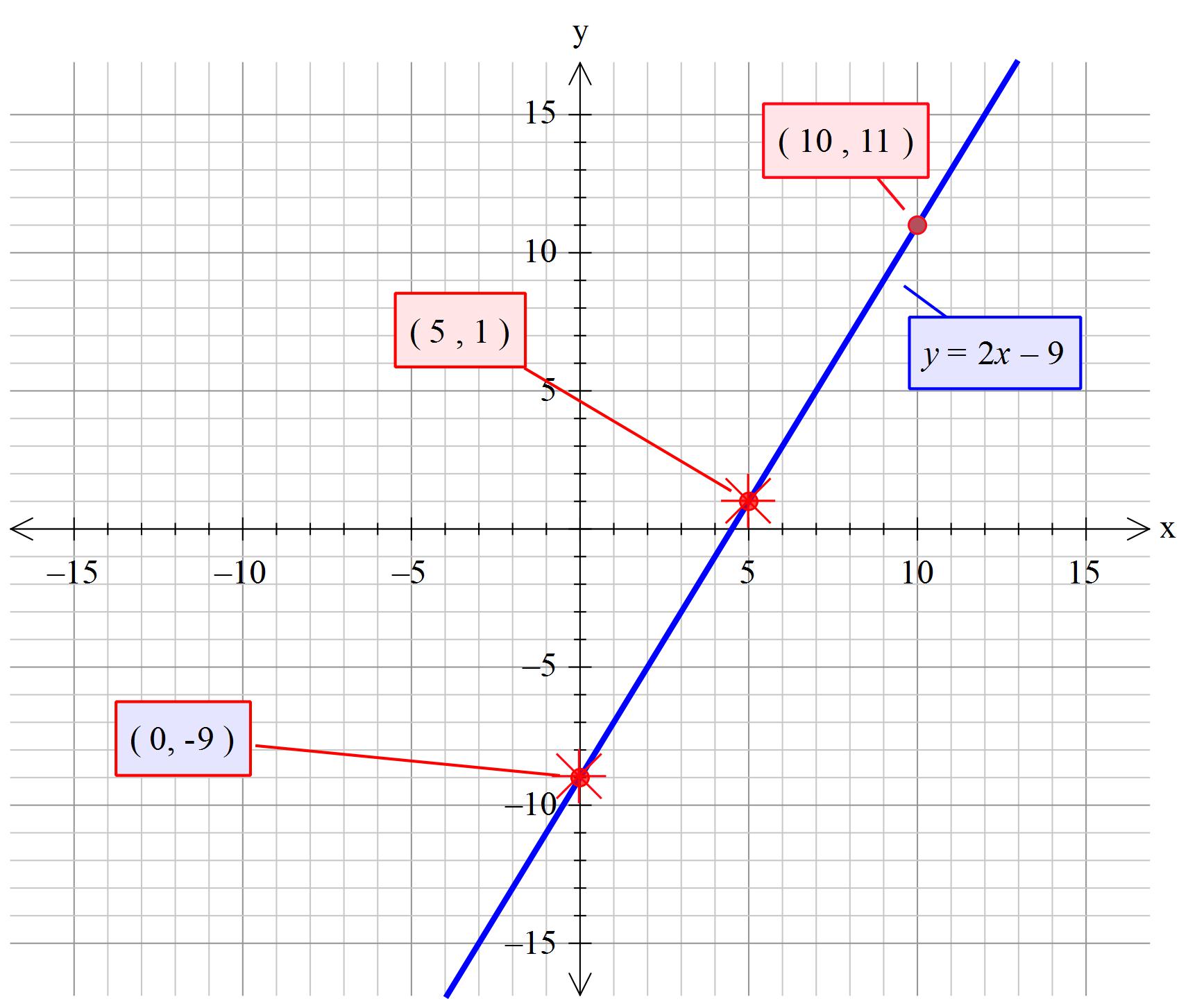



How Do You Graph Y 2x 9 Example




How To Graph Cubics Quartics Quintics And Beyond Video Lesson Transcript Study Com




Graphing Linear Inequalities




Basic Algebra Graphing Xy Points Shmoop
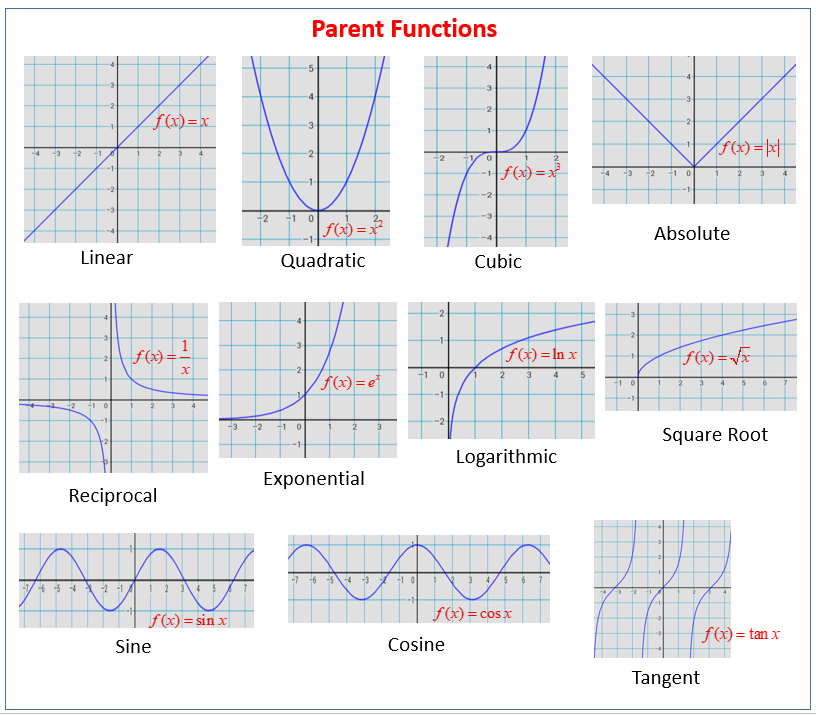



Parent Functions And Their Graphs Video Lessons Examples And Solutions




Systems Of Equations With Graphing Article Khan Academy



Quadratics Graphing Parabolas Sparknotes




Graphing Linear Inequalities
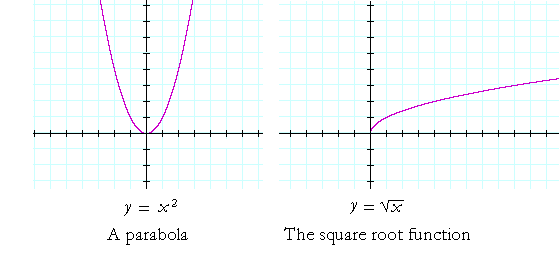



Graph Of A Parabola Topics In Precalculus



Solution How Do You Graph Y X
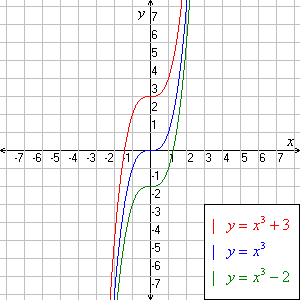



Cubic Functions



Graph Domain And Range Of Absolute Value Functions




Graph Of Y X And Y F X In Example 9 Download Scientific Diagram




Graphs For Physics Curved Graphs The Fizzics Organization



1
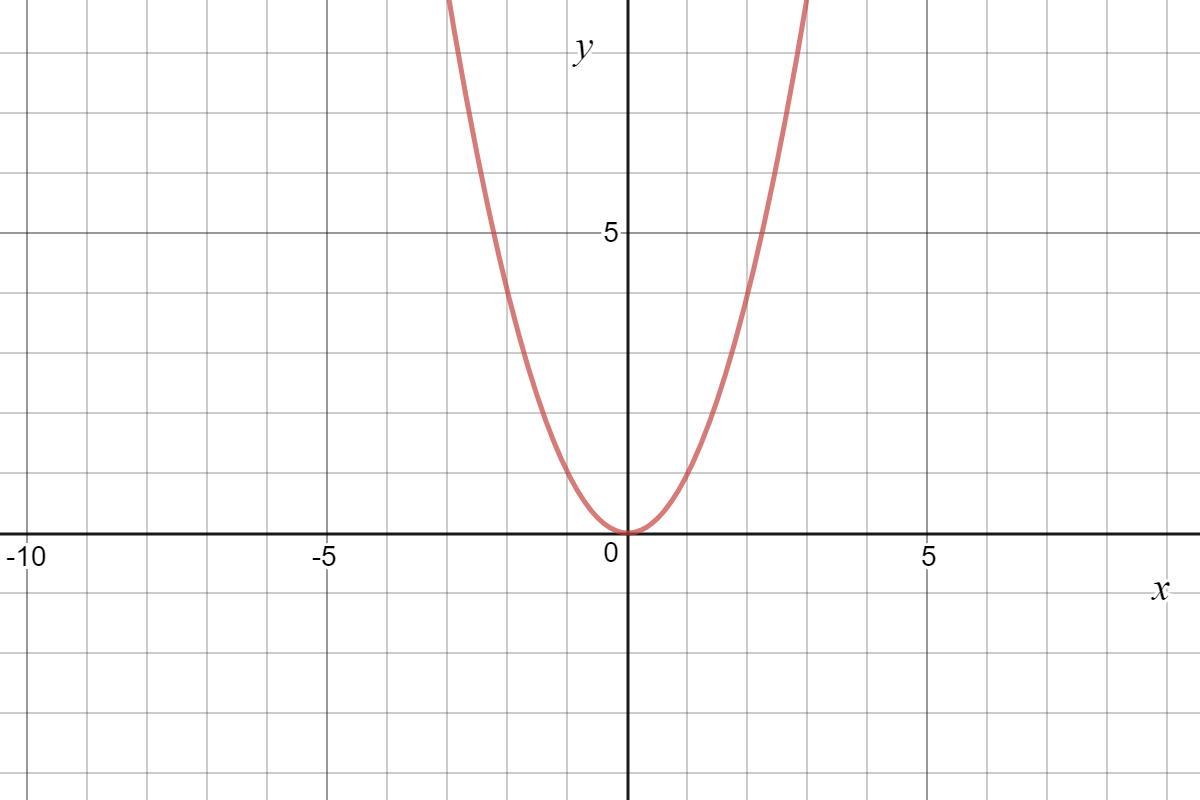



Quadratic Graph Example Y Ax C Expii
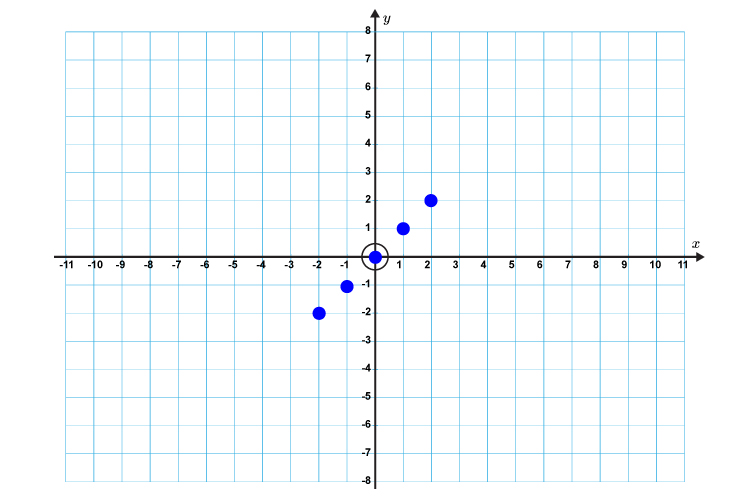



Difficult Examples Of Plotting Lines Mammoth Memory Maths
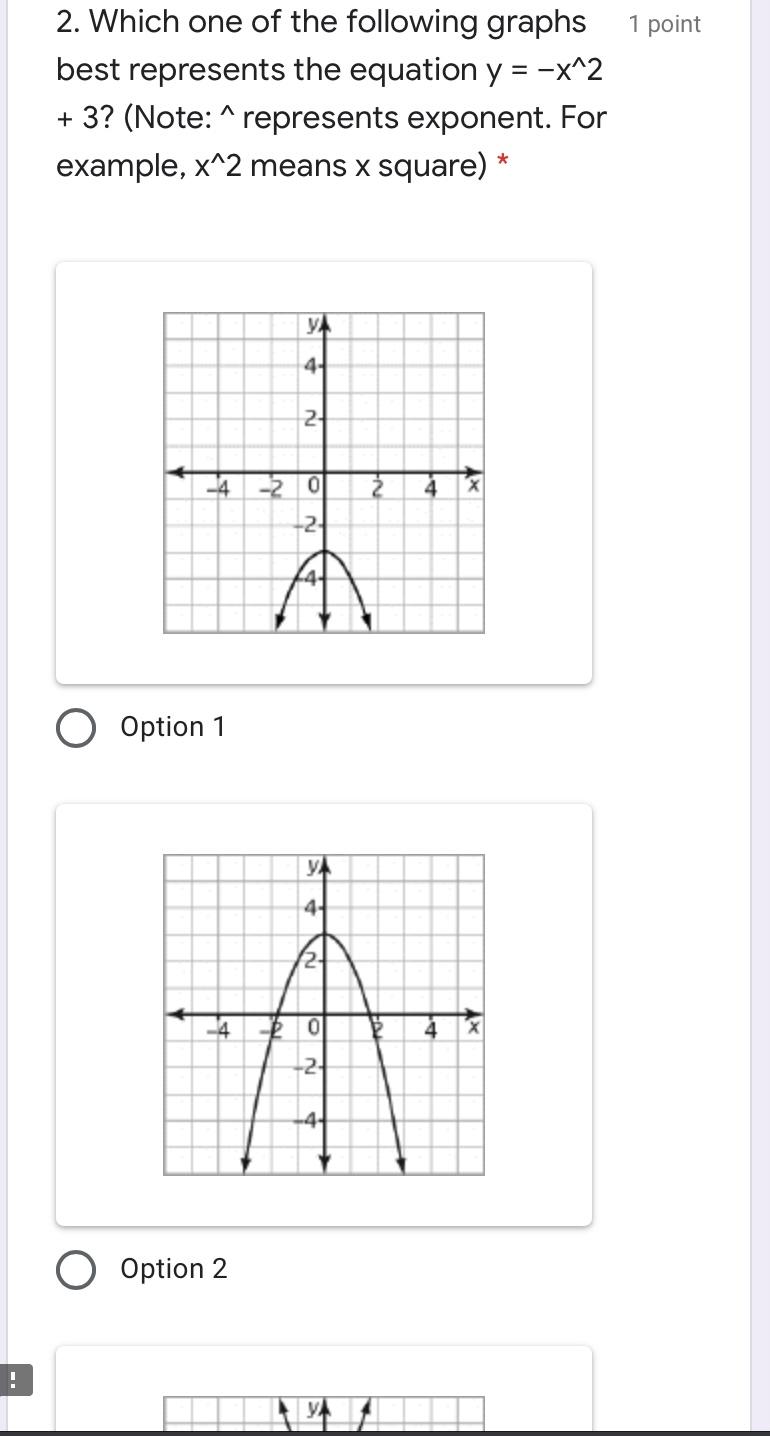



Solved 1 Point 2 Which One Of The Following Graphs Best Chegg Com




X And Y Graph Definition Differences Equation On X And Y Graph Examples



How Do You Graph The Function Y X 3 Socratic




X And Y Axis In Graph Cuemath
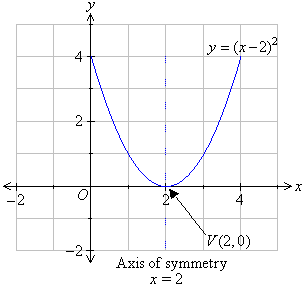



Quadratic Graphs Of Y A X B A 0




How To Draw Y 2 X 2 Interactive Mathematics




Graph Of An Approximation Of Y X Of Example 7 3 For All Download Scientific Diagram




The Characteristics Of The Graph Of A Reciprocal Function Graphs And Functions And Simultaneous Equations




The Characteristics Of The Graph Of A Reciprocal Function Graphs And Functions And Simultaneous Equations




Mathwords Graph Of An Equation Or Inequality
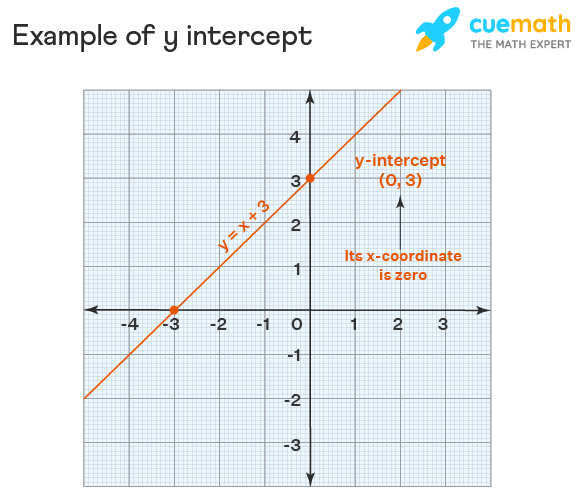



Y Intercept Meaning Examples Y Intercept Formula



Graphing Linear Inequalities



Graph Equations System Of Equations With Step By Step Math Problem Solver




Determining If Graphs Have Symmetry With Respect To The X Axis Y Axis Or Origin Precalculus Study Com




Content Transformations Of The Parabola
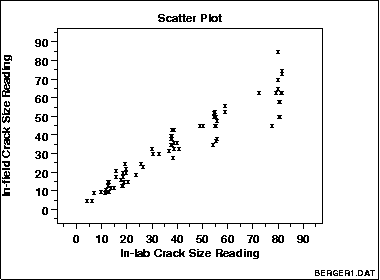



1 3 3 26 Scatter Plot
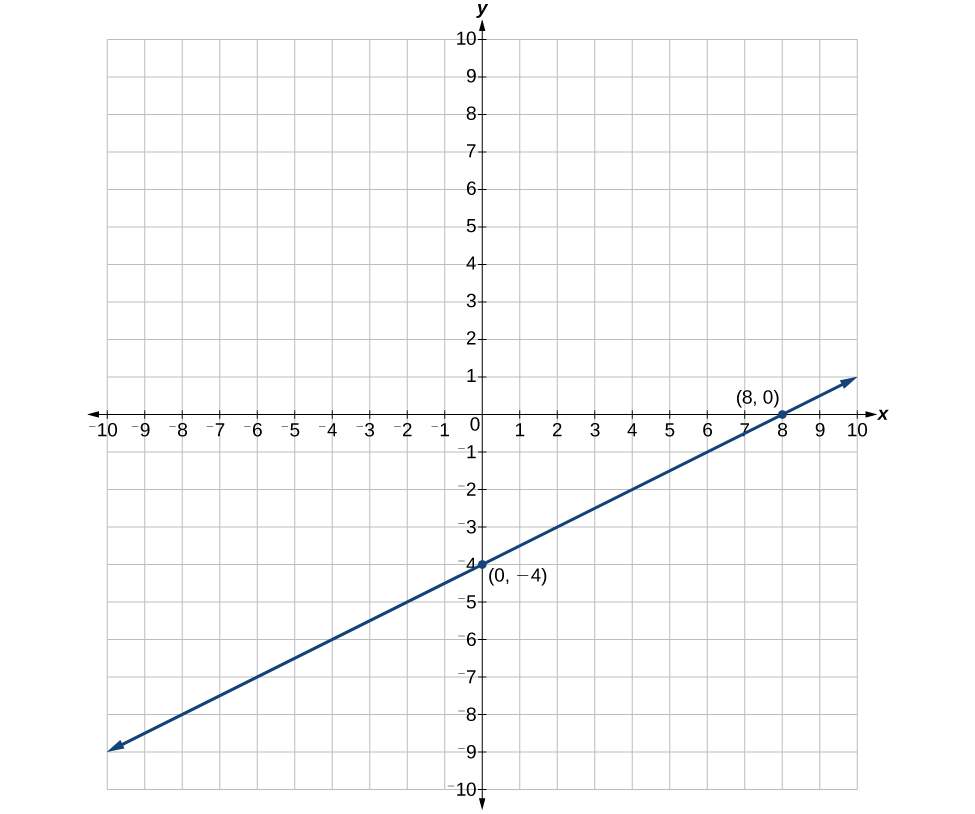



0 7 Exercises Graphing And Intercepts Finite Math
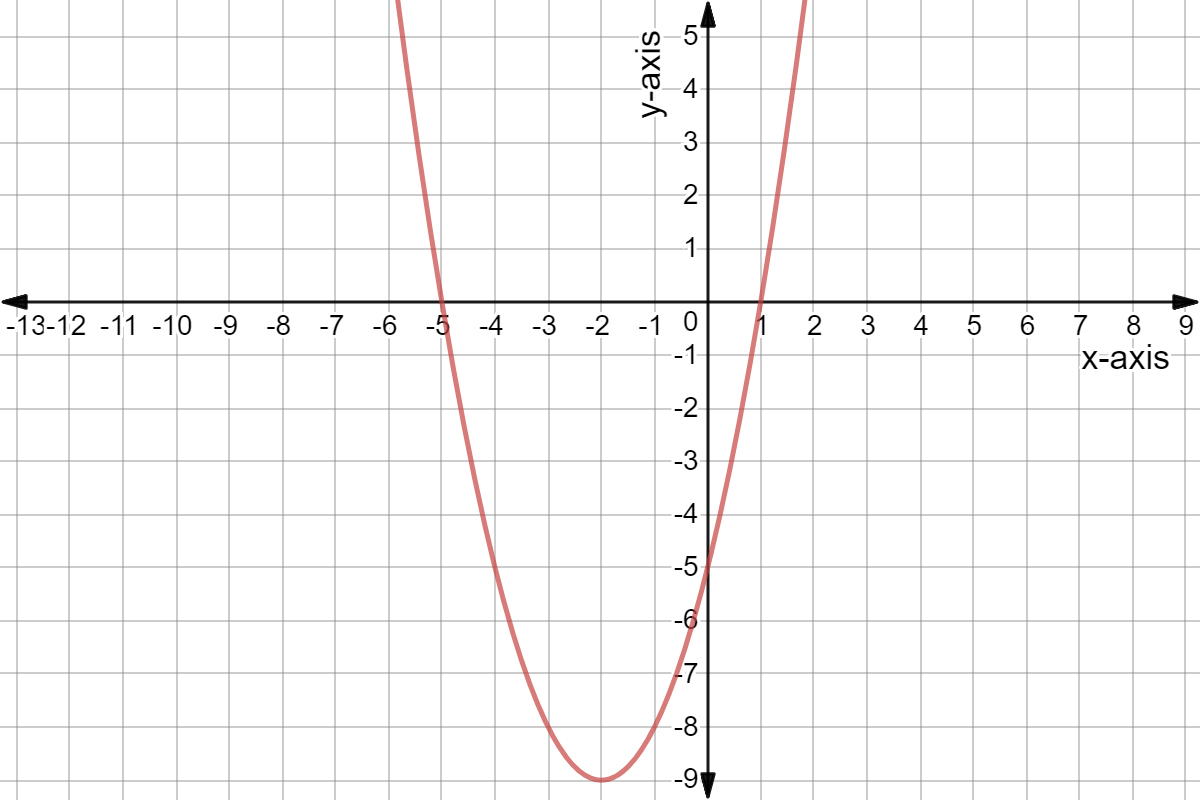



Solving Quadratic Equations By Graphing Examples Practice Expii
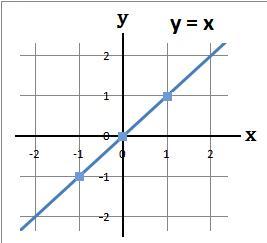



Developmaths Com High School Maths




Vertical And Horizontal Transformations Read Algebra Ck 12 Foundation
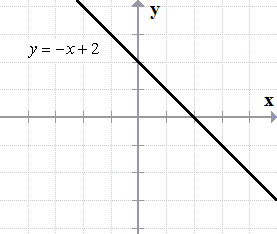



Graphing Linear Inequalities Examples Chilimath
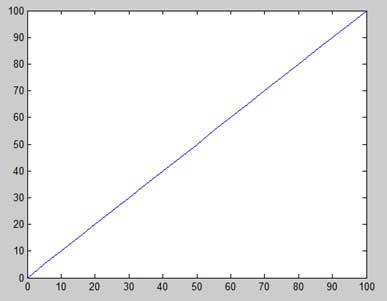



Matlab Plotting
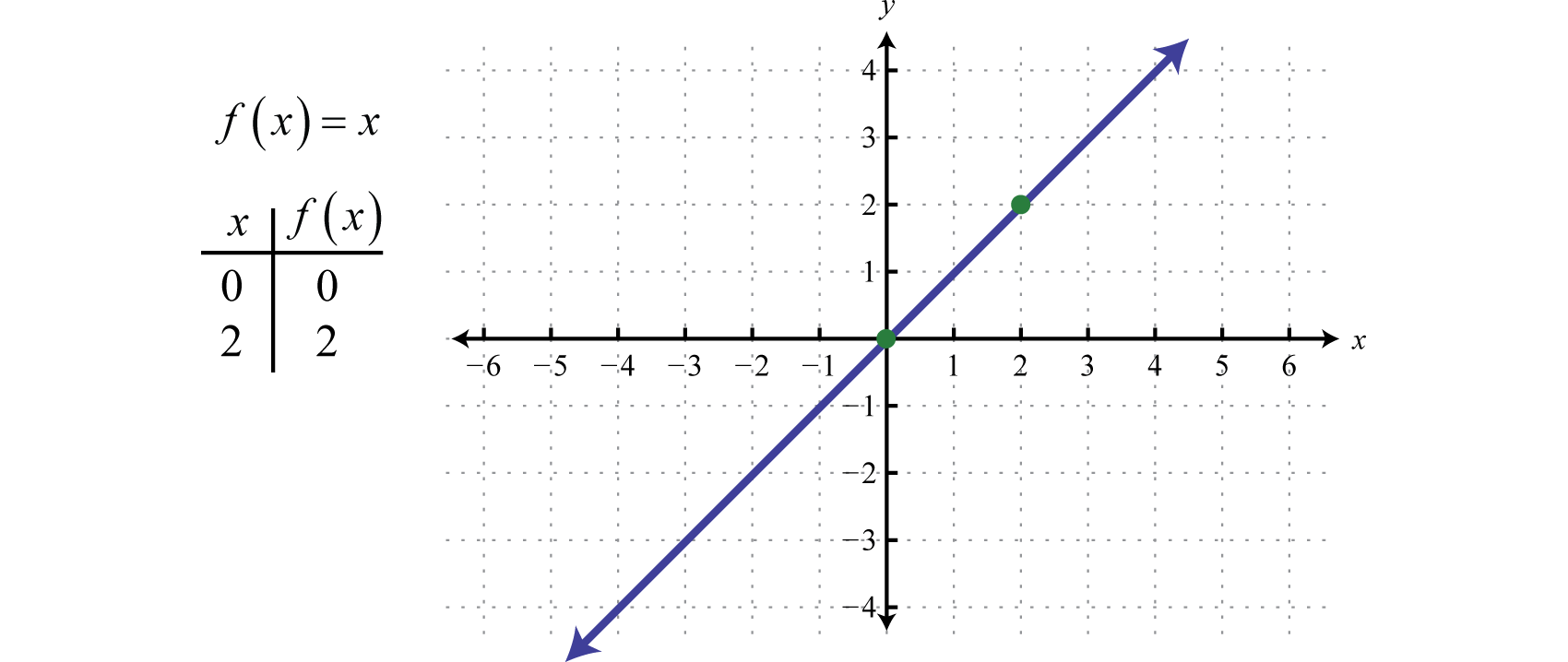



Graphing The Basic Functions
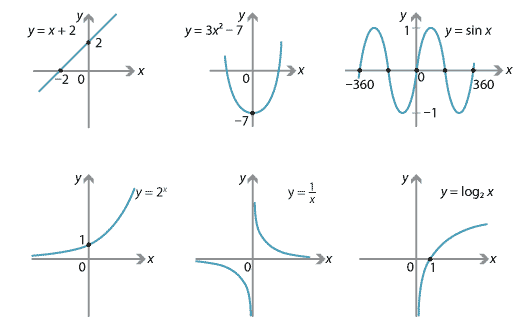



Content The Concept Of A Function




Teaching X And Y Axis Graphing On Coordinate Grids Houghton Mifflin Harcourt
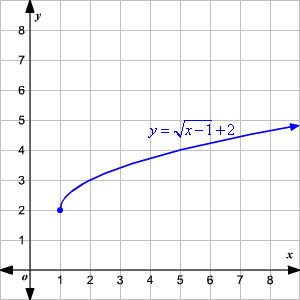



Graphing Square Root Functions
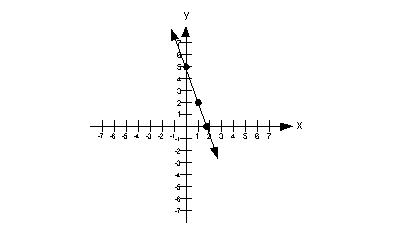



Graph Each Linear Function By Finding X And Y Intercepts




Graph Of An Approximation Of Y X Of Example 7 1 For All Download Scientific Diagram



Graphing Systems Of Linear Equations



Graphing Linear Inequalities
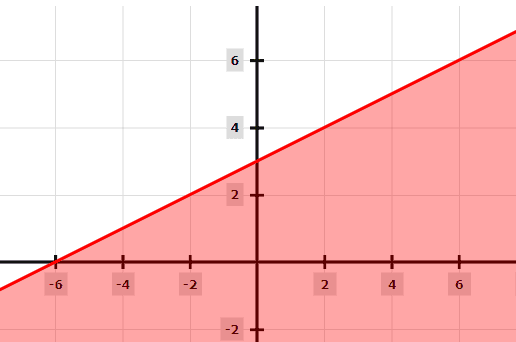



Graphing Linear Inequalities Explanation Examples



How Do You Graph The Function Y X Example



Quadratics Graphing Parabolas Sparknotes
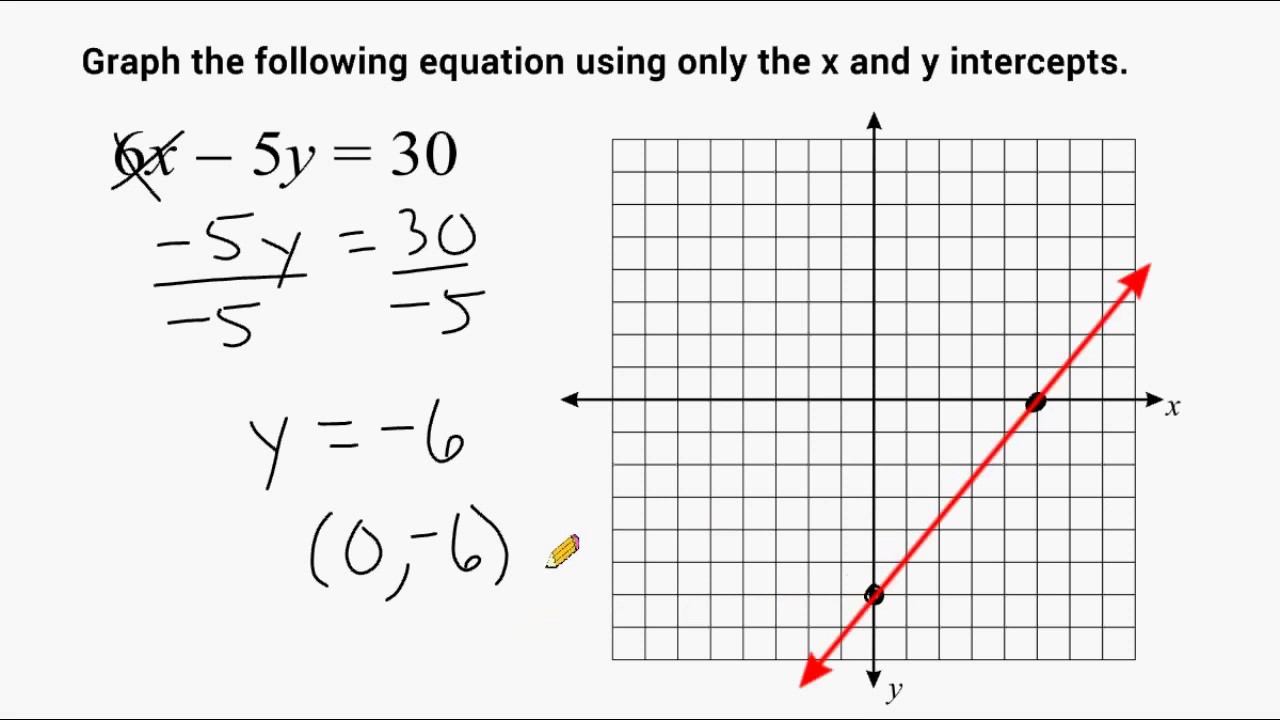



Graphing A Line Using The X And Y Intercepts Youtube
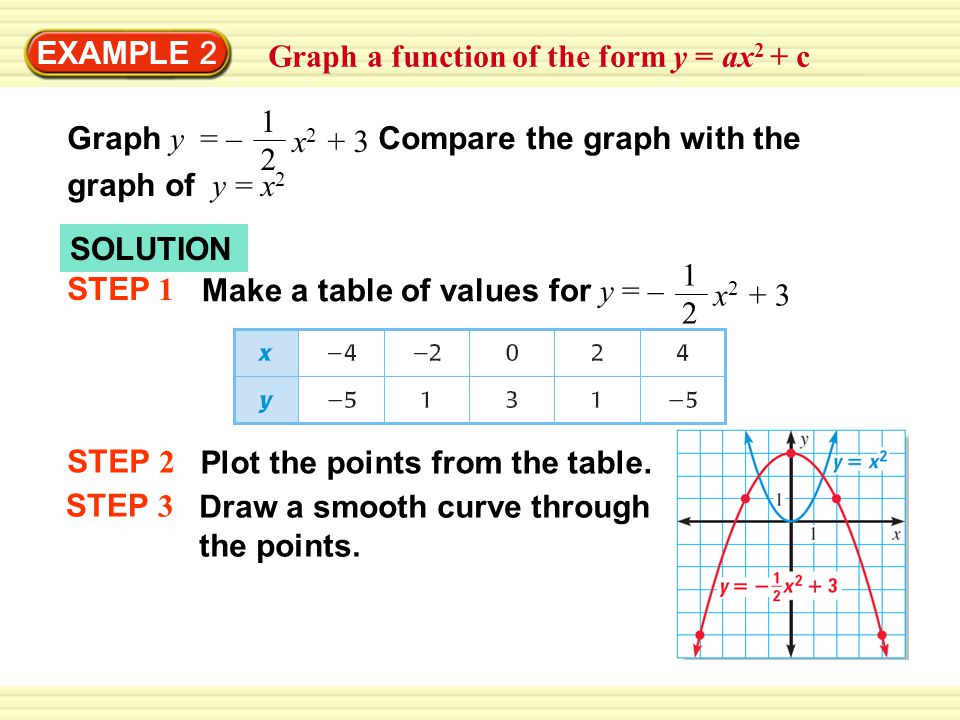



Example 1 Graph A Function Of The Form Y Ax 2 Graph Y 2x 2 Compare The Graph With The Graph Of Y X 2 Solution Step 1 Make A Table Of Values For Ppt Download



Linear Equations In The Coordinate Plane Algebra 1 Visualizing Linear Functions Mathplanet



2d Graphs



Math Parent Graphs Of 7 Equations



Graphs Of Exponential And Logarithmic Functions Boundless Algebra



Graphing Y A X H K Youtube




Graph Using Intercepts



Solved 1 Y X 8x2 5x 3 A Graph Y Be Sure To Chegg Com



Quadratic Functions




Graphing Parabolas
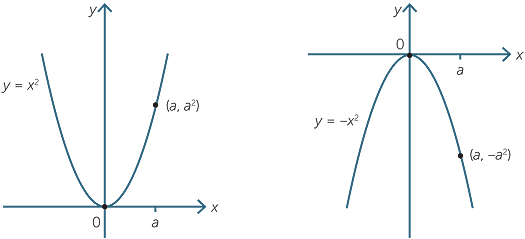



Quadratic Function



How Do You Graph The Line Y X 2 Example



Quadratics Graphing Parabolas Sparknotes



0 件のコメント:
コメントを投稿